Base canónica

Otras acepciones: Base usual.Base ortonormal 
[ENGLISH]Standard basis.Canonical basis.Natural basis. 

En álgebra lineal, sea un espacio vectorial euclídeo sobre un cuerpo de escalares $\mathbb {R}$ o $\mathbb {C}$ , la base canónica o base usual es el conjunto constituido por uno a tres vectores unitarios y directores en cada una de las rectas ortogonales que compo- nen el sistema de referencia cartesiano.

Su notación es ${\mathcal {B}}$= { i, j, k } para el espacio $\mathbb {R} ^{3}$.

Sus coordenadas en $\mathbb {R} ^{3}$ son respectivamente {(1,0,0);(0,1,0);(0,0,1)}

Cada vector a en tres dimensiones es una combinación lineal de los vectores que forman la base canónica i, j y k.

La base canónica genera un espacio vectorial ortonormal. Establecido el espacio vectorial real $\mathbf {V^{3}(\mathbb {R} )}$, tomaremos los subespacios de dimensión inferior e igual a tres a los que llamaremos euclídeos para dotarlos de la base canónica o usual ijk.

El subespacio vectorial de la recta afín

Una recta (la llamamos ${\overline {XX'}}\;$) está formada por un entramado infinito de puntos, si asociamos un vector director $\mathbf {i}$ a dicha recta. Cualquier vector contenido en ${\overline {XX'}}\;$ tendrá la forma:

$\mathbf {v} =\lambda \cdot \mathbf {i}$     $\forall {\overrightarrow {v}}\in \mathbb {V}$ , $\forall \lambda \in \mathbb {R}$ 

siendo el parámetro λ un número real que multiplicado por el vector canónico $\mathbf {i}$ genera cualquier vector contenido en dicha recta.

El número real λ a través de la operación producto de un escalar por un vector genera un conjunto de infinitos vectores, todos ellos, pertenecientes al subespacio vectorial real $\mathbb {V}$, el vector $\mathbf {i}$ al tener de módulo la unidad, realiza conversiones de escalares a vectores de la siguiente forma:

• Módulo de $\mathbf {v} \Rightarrow ||{\overrightarrow {v}}\|=\lambda$

• Dirección: Otorgado por el vector $\mathbf {i}$ , al ser director de la recta XX', tiene la misma dirección que dicha recta, en caso de vector libre, paralelo a dicha recta.

• Sentido: Otorgado por el escalar λ y en función del signo que tenga

  λ > 0 $\Rightarrow$  $\mathbf {v} =\lambda \cdot \mathbf {i}$ > 0  y su sentido es hacia la derecha de la recta: X

  λ < 0 $\Rightarrow$  $\mathbf {v} =\lambda \cdot \mathbf {i}$ < 0 y su sentido es hacia la izquierda de la recta: X'

Por otro lado, es inevitable la existencia del vector $\mathbf {0}$, cuando λ = 0, el vector nulo es un vector especial ya que carece de módulo, en consecuencia, su dirección y su sentido podría ser cualquiera, es una anomalía algebráica necesaria para fun- damentar la estructura, ya que es consecuencia inmediata de la existencia del número cero.

Isomorfía fundamental: metrización de la recta

La recta real en el eje de abscisas

Decir vector es decir punto y decir punto es decir número real, ya que existen isomorfías entre estos conjuntos numérico-geométricos:

${\overline {\mathbb {XX'} }}\thickapprox \mathbb {V} \thickapprox \mathbb {R}$

${\overline {\mathbb {XX'} }}$ ={conjunto de puntos que componen la recta ${\overline {XX'}}\;$} = {eje de abscisas}

$\mathbb {V}$ = {conjunto de los vectores contenidos en la recta}

$\mathbb {R}$ ={conjunto de los números reales}

$\mathbb {V}$ tiene estructura de espacio vectorial de dimensión unitaria sobre el cuerpo $\mathbb {R}$, sólamente requiere un sólo vector para constituir su base. Este vector puede generar la totalidad de los vectores que forman ese espacio (como estructura algebráica).

Cualquier vector director de la recta es base, pero la base canónica es la otorgada por el vector $\mathbf {i}$ cuya única coordenada es (+1). El vector $\mathbf {i}$ induce la metrización de la recta, es un segmento unidad que partiendo de un punto arbitrario O al que llamaremos origen y conveniendo que a la derecha se desplaza hacia el cono positivo de la recta en dirección a X [el cono positivo es la semirrecta OX'] y a la izquierda del origen, se desplaza hacia el cono negativo de la recta en dirección a X' [el cono negativo es la semirrecta OX']

Cualquier punto de la recta reglada puede ser identificado por un número real, siendo el número cero, el origen de las coordenadas y el 1, donde acaba el vector $\mathbf {i}$ puesto que por definición, el vector $\mathbf {i}$ es el segmento comprendido entre 0 y 1, que está orientado hacia la derecha o cono positivo.

El vector opuesto $\mathbf {-} i$ será el segmento unidad comprendido entre 0 y -1, orientado hacia la izquierda o cono negativo y cuya coordinada en este subespacio es (-1).

Cualquier número real multiplicado por el vector canónico respresentará a dicho número en la recta real y todos y cada uno de los números reales, quedan representados por un punto en esta recta.

La recta real es densa, porque a cada punto de la misma le corresponde un número real, por lo que el cardinal de ambos conjuntos es el mismo (por su isomorfía) que se establece en Alef 1 [$\aleph _{1}$](es un tipo de infinito no numerable)

La recta real

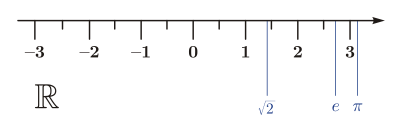
Ejemplo de vectores y números reales en la recta ${\overline {XX'}}\;$} (las coordenadas están expresadas para el plano cartesiano o afín):

$+3{\overrightarrow {i}}=(3,0)\rightarrow 3$

$-8{\overrightarrow {i}}=(-8,0)\rightarrow -8$

${\sqrt {2}}{\overrightarrow {i}}=({\sqrt {2}},0)\rightarrow {\sqrt {2}}$

$\forall +3{\overrightarrow {i}};-8{\overrightarrow {i}};{\sqrt {2}}{\overrightarrow {i}}\in \mathbb {V} (\mathbb {R} )$

La recta real en el eje de ordenadas

Este mismo subespacio vectorial $[\mathbb {V} (\mathbb {R} )]$ es trasladable a otra recta, que llamamos ${\overline {YY'}}$ esta recta, por definición, será ortogonal a ${\overline {XX'}}$ y ambas se cortarán en el origen O.

${\overline {\mathbb {YY'} }}$ ={conjunto de puntos que componen la recta ${\overline {YY'}}\;$} = {eje de ordenadas}

En la recta ${\overline {\mathbb {YY'} }}$, el cono positivo estará situado en la parte superior del origen y el cono negativo lo estará en la parte inferior del origen.

El vector canónico para esta recta se llama $\mathbf {j}$

Igualmente, al tratarse del mismo subespacio trasladado a otra recta, cumple también la isomorfía general:

${\overline {\mathbb {YY'} }}\thickapprox \mathbb {V} \thickapprox \mathbb {R}$

Ejemplo de vectores y números reales en la recta ${\overline {YY'}}\;$} (las coordenadas están expresadas para el plano cartesiano o afín):

$+3{\overrightarrow {j}}=(0,3)\rightarrow 3$

$-8{\overrightarrow {j}}=(0,-8)\rightarrow -8$

${\sqrt {2}}{\overrightarrow {j}}=(0,{\sqrt {2}})\rightarrow {\sqrt {2}}$

$\forall +3{\overrightarrow {j}};-8{\overrightarrow {j}};{\sqrt {2}}{\overrightarrow {j}}\in \mathbb {V} (\mathbb {R} )$

Subespacio vectorial del plano: El plano afín

Un plano está formado por un entramado infinito de rectas, vamos a llamar $\mathbb {X} Y$ al plano que contiene dos rectas significativas, escogidas de entre todas las que hay, una es ${\overline {XX'}}$ y otra, a la que llamamos ${\overline {YY'}}$ y que entre sí son ortogonales (En otras palabras: que forman ángulo recto o que son perpendiculares) y se cortan por un punto, al que llamamos origen y denotamos O.

Cada uno de los ejes coordenados es un subespacio vectorial de dimensión unitaria.

El producto cartesiano $\mathbb {V}$ X $\mathbb {V}$ es a su vez, un subespacio vectorial, pero la dimensión es 2. La metrización de las rectas generatrices quedaría trasladada a este plano, al que se denomina plano afín

Podemos establecer un isomorfismo entre este plano $\mathbb {X} Y$ y el conjunto producto cartesiano V x V

Cada punto de dicho plano quedaría señalado por un vector posición que partiendo del origen, llegase a dicho punto.

Sea dicho punto, el punto P, el vector posición sería OP.

Tanto el punto P, como el vector OP compartirían las mismas coordenadas (x, y) donde 'x' será la distancia al origen en el eje de abscisas e 'y' lo mismo para el eje de ordenadas.

YY' es un subespacio vectorial de la recta, de dimensión 1 y con la base canónica formada por el vector j.

Ahora, en este nuevo subespacio, de dimensión 2, al que vamos a denominar V^2(R), la base canónica está formada por los vectores { i, j},tomando coordenadas en V^2 es: i = (1, 0) j = (0, 1)

Esta base canónica es suficiente para generar todos los vectores del plano en la forma:

u = λi + μj

Espacio vectorial real euclídeo tridimensional

El espacio tridimensional está formado por un entramado infinito de planos. Escogemos un plano al que llamaremos XY, le asociaremos la base canónica $V^{2}$ para el espacio compuesta por los vectores: {i = (1, 0, 0), j = (0, 1, 0)}. Esta base sóla- mente nos puede generar vectores que estén dentro del plano o que exterior a éste, sean paralelos.

Para poder generar el resto de los vectores del espacio, debemos de tomar un vector, que siendo normal al plano (perpendicular, ortogonal), sea unitario. El único vector que cumple estas condiciones es el vector k = (0, 0, 1).

Ahora, una combinación lineal de los vectores ijk podrá generar cualquier vector del espacio:

u = λi + μj + vk

Necesariamente este vector k deberá ser director de la recta ZZ'.Otra notación para la base canónica cartesiana es:

$\mathbf {e} _{x}=(1,0,0),\quad \mathbf {e} _{y}=(0,1,0),\quad \mathbf {e} _{z}=(0,0,1).$

El conjunto de todos estos vectores de un mismo espacio se denota como V^3

La dimensión de V es 3 (largo, ancho y alto), Se requieren tres vectores para generar a todos los demás, cualquier trío de vectores linealmente independientes conforman una base del espacio vectorial V^3

Temas relacionados

• Vector (física)
• Espacio vectorial
• Combinación lineal
• Independencia lineal
• Base (álgebra)
• Base Ortogonal
• Base Ortonormal
• Coordenadas cartesianas
• Producto escalar

Referencias

• Lozano Lucea,J.J. y Vigatá Campo,J.L. Cálculo con vectores (Física 1 -Cuadernos de COU y selectividad) — Madrid:1992. - Editorial Alhambra Longman,S.A. - Primera edición. ISBN: 84-205-2122-1.

• Lipschutz, Seymour. Álgebra lineal (McGrawHill). Madrid 1.992.Editorial McGraw-Hill Interamericana de España, S.A.U.- Segunda edición. ISBN:84-7615-758-4.