Teorema del valor medio

En cálculo diferencial, el teorema de valor medio (de Lagrange), también llamado teorema de los incrementos finitos , teorema de Bonnet-Lagrange o teoria del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante de cálculo (ver también el teorema fundamental del cálculo integral). El teorema no se usa para resolver problemas matemáticos; más bien, se usa normalmente para probar otros teoremas. El teorema de valor medio puede usarse para demostrar el teorema de Taylor ya que es un caso especial.

Enunciado para una variable

Para una función que cumpla la hipótesis de ser definida y continua [a, b] y derivable en el intervalo abierto (a, b) entonces existe al menos algún punto c en el intervalo (a, b) en que la pendiente de la curva es igual que la pendiente media de la curva en el intervalo cerrado [a, b].

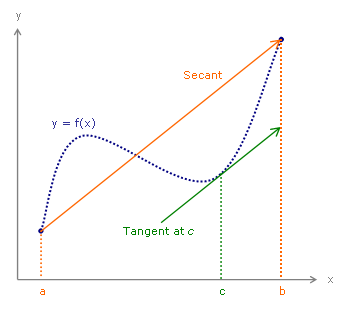
En esencia el teorema dice que dada cualquier función f continua en el intervalo [a, b] y diferenciable en el intervalo abierto (a, b) entonces existe al menos algún punto c en el intervalo (a, b) tal que la tangente a la curva en c es paralela a la recta secante que une los puntos (a, f(a)) y (b, f(b)). Es decir:

$f(b)-f(a)=f'(c)(b-a)\qquad$

Este teorema lo formuló Lagrange.

El teorema del valor medio de Lagrange de hecho es una generalización del teorema de Rolle que dice que si una función es definida y continua [ a , b ], diferenciable en el intervalo abierto ( a , b ) , y toma valores iguales en los extremos del intervalo --en otras palabras, f ( a ) = f ( b )-- entonces existe al menos algún punto c en el intervalo ( a , b ) tal que la tangente a la curva en c es horizontal, es decir f '( c)=0.

Demostración

El conocimiento del significado de la derivada de una función en un punto, y de la ecuación punto-pendiente de una recta, permiten deducir que la ecuación de la recta tangente en un punto de la curva es:

$y=f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)$

Donde los pares de puntos $(a,f(a))\;$ y $(b,f(b))\;$ son una pareja cualquiera de puntos de la curva. Vamos a demostrar que, una vez conocida una pareja de puntos de una curva continua y derivable, existe un punto c contenido en el intervalo (a,b) tal que la pendiente en dicho punto es paralela a la recta que une los puntos (a, f(a)) y (b, f(b)). Definimos una función:

$g(x)=f(x)-y=f(x)-[f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)]$

Puesto que f es continua en [a, b] y diferenciable en (a, b), lo mismo se puede decir de g. Además g satisface las condiciones del Teorema de Rolle ya que:

$g(a)=g(b)\qquad \Rightarrow \qquad f(a)-f(a)-{\frac {f(b)-f(a)}{b-a}}(a-a)=f(b)-f(a)-{\frac {f(b)-f(a)}{b-a}}(b-a)$

Por el Teorema de Rolle, como g es derivable en (a, b) y g(a)=g(b), existe un c perteneciente (a, b) tal que g '(c) = 0, y por tanto:

$0=g'(c)=f'(c)-{\frac {f(b)-f(a)}{b-a}}$

y así

$f'(c)={\frac {f(b)-f(a)}{b-a}}$

como queríamos demostrar.

Forma Integral del Teorema del Valor Medio

$f(c)={\frac {1}{(b-a)}}\int _{a}^{b}f(x)\,dx$

Enunciado para varias variables

Sea $A\subset \mathbb {R} ^{n}$ un conjunto abierto y convexo y $f:A\longrightarrow \mathbb {R}$ una función real diferenciable sobre ese abierto. Entonces se tiene que:​

$f(\mathbf {b} )-f(\mathbf {a} )=Df(\mathbf {c} )(\mathbf {b} -\mathbf {a} )$

Donde:

$Df(\mathbf {c} )$, es la aplicación lineal que representa el jacobiano (gradiente).

$\mathbf {c} =\mathbf {a} +\theta (\mathbf {b} -\mathbf {a} )$

$0\leq \theta \leq 1\;$

Generalizaciones

No existe un análogo estricto del teorema de valor medio para aplicaciones $\mathbf {f} :A\longrightarrow \mathbb {R} ^{n}$. En este caso, sólo es posible establecer la siguiente desigualdad en términos de la norma:

$\|\mathbf {f} (\mathbf {b} )-\mathbf {f} (\mathbf {a} )\|\leq \|\left(D\mathbf {f} (\mathbf {c} )\right)(\mathbf {b} -\mathbf {a} )\|\leq \|D\mathbf {f} (\mathbf {c} )\|\|(\mathbf {b} -\mathbf {a} )\|$

Demostración

En efecto teniendo en cuenta que dada una función $\mathbf {f} :A\subset \mathbb {R} ^{n}\longrightarrow \mathbb {R} ^{m}$ [1] $\ \|\int _{0}^{1}f(t)\,dt\|\leq \int _{0}^{1}\|f(t)\|\,dt$ se tiene que si $\ I[x,y]$ es el segmento formado por $\ x,y\in A$ (siendo A conexo y abierto), es $\ I[x,y]\subset A$ y entonces $\ \|f(y)-f(x)\|=\|\int _{0}^{1}df(x(1-t)+ty)(y-x)\,dt\|\leq \int _{0}^{1}\|df(x(1-t)+ty)(y-x)\|\,dt$ de donde se tiene que como $\ \|df(x(1-t)+ty)(y-x)\|\leq \|df(x(1-t)+ty)\|\|y-x\|$ $\ \forall t\in [0,1]$ es $\ \|f(y)-f(x)\|\leq \|df(c)\|\|y-x\|$ para algún $\ c\in I(x,y)$ Para ver [1] basta tener en cuenta que si $\ L=\int _{0}^{1}f(t)\,dt$ $\ \|L\|^{2}=\|\int _{0}^{1}f(t)\,dt\|^{2}=<L,\int _{0}^{1}f(t)\,dt>=\int _{0}^{1}<L,f(t)>\,dt\leq \int _{0}^{1}\|L\|\|f(t)\|dt=\|L\|\int _{0}^{1}\|f(t)\|dt$ y se tiene que $\ \|\int _{0}^{1}f(t)\,dt\|\leq \int _{0}^{1}\|f(t)\|\,dt$

Referencias

• Bombal, Marin & Vera: Problemas de Análisis matemático: Cálculo Diferencial, 1988, ed. AC, ISBN 84-7288-101-6.