Diferencia entre revisiones de «Interpretación de Bohm»

← Ir a diferencia anterior Ir a siguiente diferencia →

Contenido eliminado Contenido añadido

En renglón

Revisión del 17:16 27 may 2010

La interpretación de Bohm (también llamada teoría de la "onda piloto" o interpretación causal) es una interpretación de la teoría cuántica postulada por David Bohm en 1952 como una extensión de la onda guía de Louis de Broglie de 1927. Consecuentemente es llamada a veces teoría de Broglie-Bohm.

La teoría tiene varias formulaciones matemáticas posibles y ha sido presentada bajo diferentes nombres.

Introducción

La interpretación es un ejemplo de teoría de variables ocultas en la que se admite que las variables ocultas pueden proveer una descripción objetiva determinística que pueda resolver o eliminar muchas de las paradojas de la mecánica cuántica, como el gato de Schrödinger, el problema de la medida, el colapso de la función de onda, etc. La teoría de Bohm además es una teoría determinista. La mayoría de las variables relativisticas (no todas) requieren, sin embargo, un sistema privilegiado de referencia. Las variables que portan el espín y los espacios curvos son posibles también en esta teoría y pueden trasladarse a la teoría cuántica de campos.

Comparación con la interpretación convencional

En el formalismo de la teoría de De Broglie–Bohm, como en el de la mecánica cuántica convencional, existe una función de onda - una función en el espacio de todas las configuraciones posibles, pero adicionalmente contiene también una configuración actual, incluso para situaciones donde no hay observador. La evolución temporal de las posiciones de todas las partículas y la configuración de todos los campos queda definida por la función de onda, que satisface la ecuación guía. La evolución temporal de la propia función de onda viene dada por la ecuación de Schrödinger como en la mecánica cuántica no-relativista.

Experimento de la doble rendija

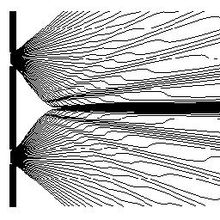
El experimento de la doble rendija es una ilustración de la dualidad onda-partícula. En él un cañón de partículas (como pej:fotones) viaja a través de una barrera con dos rendijas. Si colocamos una pantalla detectora en el otro lado, el patrón de las partículas detectadas muestra las franjas de interferencia característico de las ondas; no obstante, la pantalla del detector responde a las partículas. El sistema exhibe el comportamiento de las ondas (patrones de interferencia) y al mismo tiempo de las partículas (puntos en la pantalla).

Si modificamos este experimento de manera que una de las rendijas está cerrada, no se observa ningun patrón de interferencia. Así el estado de ambas rendijas afecta al resultado final. Podemos también colocar un detector mínimamente invasivo en una de las rendijas para saber a través de qué rendija pasó la partícula. Si hacemos esto, los patrones de interferencia también desaparecen.

La Interpretación de Copenhague establece que las partículas no poseen una localización en el espacio antes del momento en el que son detectadas, de manera que si no hay detector alguno en las rendijas carece de sentido el hecho y la pregunta de a través de qué rendija ha pasado la partícula. Si una rendija posée un detector, entonces la función de onda colapsa debido a la detección.

En la teoría de Broglie–Bohm, la función de onda viaja a través de ambas rendijas, pero cada partícula posee una trayectoria bien definida y pasa exactamente a traves de una de las dos rendijas. La posición final de la partícula en la pantalla del detector y la rendija exacta a través de la cual pasa la partícula está determinada por la posición inicial de la partícula. Tal posición inicial de la partícula no es controlable por los experimentos, de manera que hay una apariencia de aleatoriedad en en el patrón de detacción. La función de onda interfiere consigo misma y guía a la partícula de tal manera que las partículas evitan las regiones en las cuales la interferencia es destructiva y son atraidas hacia las regiones donde la interderencia es constructiva produciendo así los patrones de interferencia en la pantalla del detector.

Para explicar el comportamiento cuando la partícula es detectada pasando por una rendija, necesitamos apreciar el rol de la funcion de onda condicional y como provoca ésta el colapso de la función de onda; esto se explica más abajo. La idea básica es que el entorno que registra la detección, separa efactivamente los dos paquetes de ondas en el espacio de configuración.

Aspectos generales

Ontología de la interpretación

La ontología de la teoría de Broglie-Bohm consiste en una configuración $q(t)\in Q$ del universo y una onda piloto $\psi (q,t)\in \mathbb {C}$ . El espacio de configuración $Q$ puede elegirse de manera diferente, como en mecanica clásica y en la mecánicqa cuántica estandar.

Así, la ontología de la teoría de la onda piloto contiene tanto la trayectoria $q(t)\in Q$ que conocemos en la mecánica clásica, como la función de onda $\psi (q,t)\in \mathbb {C}$ de la teoría cuántica. Así, en cada momento no solo tenemos una función de onda sino que también existe una configuración bien definida del universo entero. La correspondencia con nuestras experiencias se produce por la identificación de la configuración de unestro cerebro con alguna parte de la configuración del universo entero $q(t)\in Q$ , tal como ocurre en la mecánica clásica.

Mientras que la ontología de la mecánica clásica resulta entonces ser parte de la ontología de la teoría de Broglie–Bohm, la dinámica es muy diferente. En mecánica clásica la aceleración de las partículas está originada por fuerzas. En la teoría de Broglie–Bohm, las velocidades de las partículas vienen dadas por la función de onda.

En lo que sigue, veremos como se establece todo esto para el caso de una partícula moviendose en $\mathbb {R} ^{3}$ y a continuación para $N$ partículas moviendose en 3 dimensiones. En la primera instancia, el espacio de configuración y el espacio real son el mismo, mientras que en la segunda el espacio real es aún $\mathbb {R} ^{3}$ , pero ahora el espacio de configuracion se convierte en $\mathbb {R} ^{3N}$ . Mientras que las posiciones de las partículas permanecen en el espacio real, el campo velocidad y las funciones de onda están sobre el espacio de configuración y es así como las partículas están entrelazadas unas con otras en esta teoría.

Extensiones a esta teoría incluyen esl espín y espacios de configuración más complicados.

Se usan variaciones de $\mathbf {Q}$ para las posiciones de las partículas mientras que $\psi$ representa el valor complejo de la función de onda sobre el espacio de configuración.

Formalismo

La teoría de Broglie–Bohm se basa en lo siguiente:

Tenemos una configuración $q$ para el universo, descrita por coordenadas $q^{k}$ , que es un elemento del espacio de configuración $Q$ . El espacio de configuración es diferente para diferentes versiones de la teoría de la onda piloto. Por ejemplo, éste puede ser el espacio de posiciones $\mathbf {Q} _{k}$ de $N$ particulas, o en el caso de teoría de campos, el espacio de las configuraciones de los campos $\phi (x)$ . La configuración se desenvuelve de acuerdo con la ecuación guía

m_{k}{\frac {dq^{k}}{dt}}(t)=\hbar \nabla _{k}\operatorname {Im} \ln \psi (q,t)=\hbar \operatorname {Im} \left({\frac {\nabla _{k}\psi }{\psi }}\right)(q,t)

.

Aquí, $\psi (q,t)$ es la función de onda estandar de valor complejo conocida en la teoría cuántica, que se desenvuelve según la ecuación de Schrödinger.

i\hbar {\frac {\partial }{\partial t}}\psi (q,t)=-\sum _{i=1}^{N}{\frac {\hbar ^{2}}{2m_{i}}}\nabla _{i}^{2}\psi (q,t)+V(q)\psi (q,t)

Esto completa la especificación de la teoría para cualquier teoría cuántica con un operador hamiltoniano de tipo $H=\sum {\frac {1}{2m_{i}}}{\hat {p}}_{i}^{2}+V({\hat {q}})$ .

Si la configuración posee una distribución de acuerdo con $|\psi (q,t)|^{2}$ en algún momento del tiempo $t$ , entonces también lo hace en cualquier otro momento temporal. Tal estado se denomina equilibrio cuántico. En un estado de equilibrio cuántico, esta teoría está de acuerdo con los resultados de la mecánica cuántica estandar.

Ecuación guía

Para una única partícula moviendose en $\mathbb {R} ^{3}$ , la velocidad de la partícula viene dada por

${\frac {d\mathbf {Q} }{dt}}(t)={\frac {\hbar }{m}}\operatorname {Im} \left({\frac {\nabla \psi }{\psi }}\right)(\mathbf {Q} ,t)$ .

Para múltiples partículas indicamos $\mathbf {Q} _{k}$ para la partícula $k$ , su velocidad viene dada por

${\frac {d\mathbf {Q} _{k}}{dt}}(t)={\frac {\hbar }{m_{k}}}\operatorname {Im} \left({\frac {\nabla _{k}\psi }{\psi }}\right)(\mathbf {Q} _{1},\mathbf {Q} _{2},\ldots ,\mathbf {Q} _{N},t)$ .

El hecho clave que debemos resaltar es que la velocidad depende de las posiciones actuales de todas las $N$ partículas del universo. Como explicamos más abajo, en la mayoría de las situaciones experimentales, la influencia de todas las partículas puede quedar encapsulada en la función de onda efectiva de un subsistema del universo.

Bohm y el problema de la medida

Esta teoría ofrece un formalismo para la medición análogo al de la termodinámica en la mecánica clásica, del que carece el formalismo estandar generalmente asociado a la Interpretación de Copenhague. El problema de la medida se resuelve muy fácilmente en esta teoría, ya que el resultado de un experimento es producido por la interacción con la configuración de las partículas del aparato de medida cuando éste se realiza. El colapso de la función de onda que en la interpretación de Copenhague debe postularse, emerge aquí de manera natural del análisis de los subsistemas bajo la hipótesis de equilibrio cuántico.

Dificultades de la interpretación

La desigualdad de Bell supone un resultado negativo para cierto tipo de teorías como la de Bohm. De hecho el descubrimiento del Teorema de Bell fue inspirado por el trabajo de David Bohm.

Dicho teorema es un teorema de imposibilidad que demuestra que no existen teorías de variables ocultas locales que sean compatibles con la mecánica cuántica. Así la interpretación de Bohm está condenada a eliminar la localidad o el deobjetividad física. La interpretación de Bohm opta por conservar la objetividad física y aceptar la no-localidad. Naturalmente la no-localidad supone cierta incoherencia con la teoría de la relatividad convencional.

La teoría de Broglie–Bohm expresa de una manera explícita la no localidad que aparece en la física cuántica. La velocidad de cualquier partícula depende del valor de la función de onda, la cual depende a su vez de la configuración global de la totalidad del universo.

Referencia

Notas

Bibliografía

Albert, David Z. (May de 1994). «Bohm's Alternative to Quantum Mechanics». Scientific American 270: 58-67.
Barbosa, G. D.; N. Pinto-Neto (2004). «A Bohmian Interpretation for Noncommutative Scalar Field Theory and Quantum Mechanics». Physical Review D 69: 065014. doi:10.1103/PhysRevD.69.065014. arΧiv:hep-th/0304105.
Bohm, David (1952). «A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables" I». Physical Review 85: 166-179. doi:10.1103/PhysRev.85.166.
Bohm, David (1952). «A Suggested Interpretation of the Quantum Theory in Terms of "Hidden Variables", II». Physical Review 85: 180-193. doi:10.1103/PhysRev.85.180.
Bohm, David (1990). «A new theory of the relationship of mind and matter». Philosophical Psychology 3 (2): 271-286. doi:10.1080/09515089008573004.
Bohm, David; B.J. Hiley (1993). The Undivided Universe: An ontological interpretation of quantum theory. London: Routledge. ISBN 0-415-12185-X.
Durr, Detlef; Sheldon Goldstein, Roderich Tumulka and Nino Zangh (December de 2004). «Bohmian Mechanics» (PDF). Physical review letters 93 (9): 090402. ISSN 0031-9007. PMID 15447078. |autor= y |apellido= redundantes (ayuda)
Goldstein, Sheldon (2001). «Bohmian Mechanics». Stanford Encyclopedia of Philosophy.
Hall, Michael J.W. (2004). «Incompleteness of trajectory-based interpretations of quantum mechanics». Journal of Physics a Mathematical and General 37: 9549. doi:10.1088/0305-4470/37/40/015. arΧiv:quant-ph/0406054. (Demonstrates incompleteness of the Bohm interpretation in the face of fractal, differentialble-nowhere wavefunctions.)
Holland, Peter R. (1993). The Quantum Theory of Motion : An Account of the de Broglie–Bohm Causal Interpretation of Quantum Mechanics. Cambridge: Cambridge University Press. ISBN 0-521-48543-6.
Nikolic, H. (2004). «Relativistic quantum mechanics and the Bohmian interpretation». Foundations of Physics Letters 18: 549. doi:10.1007/s10702-005-1128-1. arΧiv:quant-ph/0406173.
Passon, Oliver (2004). Why isn't every physicist a Bohmian?. arΧiv:quant-ph/0412119.
Sanz, A. S.; F. Borondo (2003). «A Bohmian view on quantum decoherence». The European Physical Journal D 44: 319. doi:10.1140/epjd/e2007-00191-8. arΧiv:quant-ph/0310096.
Sanz, A.S. (2005). «A Bohmian approach to quantum fractals». J. Phys. A: Math. Gen. 38: 319. doi:10.1088/0305-4470/38/26/013. (Describes a Bohmian resolution to the dilemma posed by non-differentiable wavefunctions.)
Silverman, Mark P. (1993). And Yet It Moves: Strange Systems and Subtle Questions in Physics. Cambridge: Cambridge University Press. ISBN 0-521-44631-7.
Streater, Ray F. (2003). «Bohmian mechanics is a "lost cause"». Consultado el 25 de junio de 2006.
Valentini, Antony; Hans Westman (2004). Dynamical Origin of Quantum Probabilities. arΧiv:quant-ph/0403034.
Bohmian mechanics on arxiv.org

@@ Línea 69: / Línea 69: @@
 La teoría de Broglie–Bohm expresa de una manera explícita la no localidad que aparece en la física cuántica. La velocidad de cualquier partícula depende del valor de la función de onda, la cual depende a su vez de la configuración global de la totalidad del universo.
-===Ecuación de Schrödinger===
-La ecuación de Schrödinger para una partícula gobierna la evolución temporal de una función de onda de valor complejo en <math>\mathbb{R}^3</math>. La ecuación representa una versión cuantizada de la energía total de un sistema clásico desenvolviendose bajo una función potencial de valor real <math>V</math> en <math>\mathbb{R}^3</math>:
-:<math>i\hbar\frac{\partial}{\partial t}\psi=-\frac{\hbar^2}{2m}\nabla^2\psi + V\psi</math>
-Para múltiples partículas, la ecuación es la misma excepto en que <math>\psi</math> and <math>V</math> están ahora sobre el espacio de configuración, <math>\mathbb{R}^{3N}</math>.
-:<math>i\hbar\frac{\partial}{\partial t}\psi=-\sum_{k=1}^{N}\frac{\hbar^2}{2m_k}\nabla_k^2\psi + V\psi</math>
-Esta es la misma función de onda de la mecánica cuántica convencional.
-===La Regla de Born===
-En los escritos originales de Bohm [Bohm 1952], el autor discute cómo la teoría de Broglie–Bohm llega a los mismos resultados en la medición que la mecánica cuántica. La idea clave es que ello sería cierto si las posiciones de las partículas satisfacen la distribución estadística dada por <math>|\psi|^2</math>. Dicha distribución queda garantizada en cualquier momento por la ecuación guía si la distribución inicial de las partículas satisface <math>|\psi|^2</math>.
-Para un experimento dado, podemos postular que esto es cierto y verificar experimentalmente que sigue siendolo, como así ocurre efectivamente. Pero, como argumentan Dürr et al.,<ref name="dgz92">Dürr, D., Goldstein, S., and Zanghì, N., [http://arxiv.org/abs/quant-ph/0308039 "Quantum Equilibrium and the Origin of Absolute Uncertainty"], Journal of Statistical Physics 67: 843&ndash;907,  1992.</ref> se necesitaría algún argumento que muestre que esta distribución es la típica para cualquier subsistema. Argumentan que <math>|\psi|^2</math> en virtud de su equivariancia bajo la evolución dinámica del sistema, es la medida apropiada de ''tipicalidad'' para las condiciones iniciales de las posiciones de las partículas. A continuación se puede probar que una inmensa mayoría de las configuraciones iniciales posibles se corresponden con la regla de Born (i.e., <math>|\psi|^2</math>) surgiendo así la estadística que muestran las medidas.  Dicho brevemente, el comportamiento según la regla de Born es típico.
-La situación es así análoga a la situación en física clásica estadística. Una situación inicial con baja entropía se convertirá con una probabilidad extremadamente alta, en un estado de mayor entropía: el comportamiento consistente con el segundo principio de la termodinámica es típico. Hay desde luego, condiciones iniciales anómalas que darían lugar a violaciones de la segunda ley.
-No obstante, careciendo de información muy detallada sobre los estados iniciales sería muy poco razonable esperar otra cosa que el incremento de la entropía que observamos actualmente. Similarmente, en la teoría de Broglie–Bohm, hay condiciones iniciales anómalas que producirían mediciones estadísticas que violarían la regla de  Born  (i.e., en conflicto con las predicciones de la teoría cuántica estandar).  Pero el teorema de ''tipicalidad'' muestra que excepto en los casos en que haya una razón particular para creer que hay unas condiciones iniciales especiales de facto, el comportamiento según la regla de Born es lo que deberíamos esperar.
-Es por ello que en un sentido cualificado, la regla de Born es un teorema en la teoría de Broglie–Bohm, mientras que en la teoría cuántica ordinaria es un postulado que tiene que ser añadido.
-===La función de onda condicional de un subsistema===
-En la formulación de la teoría de Broglie–Bohm, solo existe una función de onda para el universo entero (que siempre se refiere a la ecuación de Schrödinger). No obstante, una vez que la teoría es formulada, es conveniente introducir la noción de función de onda también para subsistemas en el universo. Si escribimos la función de onda para el universo como <math>\psi(t,q^{\mathrm I},q^{\mathrm{II}})</math>, donde <math>q^{\mathrm I}</math> denota las variables de configuración asociadas a algún subsistema (I) del universo y <math>q^{\mathrm{II}}</math> denota las variables de configuración restantes. Denota, respectivamente, por <math>Q^{\mathrm I}(t)</math> y por <math>Q^{\mathrm{II}}(t)</math> la configuración actual del subsistema (I) y del resto del universo. Por simplicidad, consideramos aquí solo el caso sin espín. La ''función de onda condicional'' del subsistema (I) se define como:
-<math>\psi^{\mathrm I}(t,q^{\mathrm I})=\psi(t,q^{\mathrm I},Q^{\mathrm{II}}(t)).</math>
-Se sigue inmediatamente del hecho de que <math>Q(t)=(Q^{\mathrm I}(t),Q^{\mathrm{II}}(t))</math> satisface la ecuación guías que también la configuración <math>Q^{\mathrm I}(t)</math> satisface una ecuación guía idéntica a la presentada en la formulación de la teoría, con la función de onda universal <math>\psi</math> reemplazada por la función de onda condicional <math>\psi^{\mathrm I}</math>. También, el hecho de que <math>Q(t)</math> es aleatoria con [[función densidad de probabilidad|densidad de probabilidad]] dada por el cuadrado del módulo de <math>\psi(t,\cdot)</math> implica que la [[densidad de probabilidad condicional]] de <math>Q^{\mathrm I}(t)</math> dada <math>Q^{\mathrm{II}}(t)</math> es dada por el cuadrado del módulo de la función de onda condicional (normalizada) <math>\psi^{\mathrm I}(t,\cdot)</math> (en la terminología de Dürr et al.<ref>Quantum Equilibrium and the Origin of Absolute Uncertainty, D. Dürr, S. Goldstein and N. Zanghì, Journal of Statistical Physics 67, 843-907 (1992), http://arxiv.org/abs/quant-ph/0308039.</ref> este hecho se llama la ''formula fundamental de la probabilidad condicional'').
-A diferencia de la función de onda universal, la función de onda condicional de un subsistema no siempre se comporta según la ecuación de Schrödinger, pero en muchas situaciones sí que lo hace. Por ejemplo, si la función de onda universal se factoriza como:
-<math>\psi(t,q^{\mathrm I},q^{\mathrm{II}})=\psi^{\mathrm I}(t,q^{\mathrm I})\psi^{\mathrm{II}}(t,q^{\mathrm{II}})</math>
-entonces la función de onda condicional de un subsistema (I) es (salvo un factor escalar irrelevante) igual a <math>\psi^{\mathrm I}</math> (esto es lo que la teoría cuántica estandar consideraría como la función de onda de un subsistema (I)). Si además, el Hamiltoniano no contiene un término de interacción entre los subsistemas (I) y (II) entonces <math>\psi^{\mathrm I}</math> satisface la ecuación de Schrödinger. Mas generalmente, se asume que la función de ondas universal <math>\psi</math> puede ser escrita en la forma:
-<math>\psi(t,q^{\mathrm I},q^{\mathrm{II}})=\psi^{\mathrm I}(t,q^{\mathrm I})\psi^{\mathrm{II}}(t,q^{\mathrm{II}})+\phi(t,q^{\mathrm I},q^{\mathrm{II}}),</math>
-donde <math>\phi</math> resuelve la ecuación de Schrödinger y <math>\phi(t,q^{\mathrm I},Q^{\mathrm{II}}(t))=0</math> para todo  <math>t</math> y <math>q^{\mathrm I}</math>. Entonces, de nuevo, la función de onda condicional para un subsistema (I) es (salvo un factor escalar irrelevante) igual a <math>\psi^{\mathrm I}</math> y si el Hamiltoniano no contiene un término de interacción entre los subsistemas (I) y (II), <math>\psi^{\mathrm I}</math> satisface la ecuación de Schrödinger.
-El hecho de que la función de onda condicional de un subsistema no siempre cumpla la ecuación de Schrödinger se relaciona con el hecho de que la regla usual del colapso postulado en la teoría cuántica estandar emerge de forma natural del formalismo Bohmiano cuando consideramos las funciones de conda condicionales de los subsistemas.
-==Extensiones==
-===Espín===
-Para incorporar el espín, la función de onda con valor escalar- complejo, es ahora un vector-complejo. El espacio de valores se llama espacio de espín; para una partícula de espín-1/2, el espacio de espín puede tomarse como <math>\mathbb{C}^2</math>.
-La ecuación guía se modifica tomando productos internos en el espacio de espín para reducir los vectores complejos a números complejos. La ecuación de Schrödinger se modifica añadiendo un término con el espín de Pauli.
-:<math>\frac{d \mathbf{Q}_k}{dt} (t) = \frac{\hbar}{m_k} Im \left(\frac{(\psi,D_k \psi)}{(\psi,\psi)} \right) (\mathbf{Q}_1, \mathbf{Q}_2, \ldots, \mathbf{Q}_N,  t)</math>
-:<math>i\hbar\frac{\partial}{\partial t}\psi=-\sum_{k=1}^{N}\frac{\hbar^2}{2m_k}D_k^2\psi + V\psi + \sum_{k=1}^{N} \mu_k \mathbf{S}^{(k)}\cdot \mathbf{B}(\mathbf{q}_k)</math>
-donde <math>\mu_k</math> es el momento magnético de la partícula <math>k</math>, <math>\mathbf{S}^{(k)}</math> es el operador apropiado de espín actuando sobre el espacio de espín de la partícula <math>k</math>, <math>D_k=\nabla_k-\frac{ie_k}{c\hbar}\mathbf{A}(\mathbf{q}_k)</math>, <math>\mathbf{B}</math> y <math>\mathbf{A}</math> son, respectivamente, el campo magnético y el potencial vector en <math>\mathbb{R}^{3}</math> (todas las otras funciones están completamente en el espacio de configuración), <math>e_k</math> es la carga de la partícula <math>k</math>, y <math>(\cdot,\cdot)</math> es el producto interno en el espacio de espín <math>\mathbb{C}^d</math>,
-:<math>(\phi,\psi) = \sum_{s=1}^d \phi_s^* \psi_s.</math>
-Como ejemplo de espacio de espín, un sistema consistente en dos partículas de espín 1/2 y una de espín 1 tiene una función de ondas de la forma <math>\psi: \mathbb{R}^{9}\times \mathbb{R} \to \mathbb{C}^{2}\otimes \mathbb{C}^{2} \otimes \mathbb{C}^{3}</math>. Esto es, su espacio de espín es de 12 dimensiones.
-===Espacio curvado===
-Para extender la teoría de Broglie–Bohm a un espacio curvado ([[Riemannian manifolds]] en lenguaje matemático), simplemente tenemos en cuenta que todos los elementos de esas ecuaciones tengan sentido, tales como gradientes y Laplacianos. Así, usamos ecuaciones que tengan la misma forma que arriba. Las condiciones topológicas y de contorno pueden aplicarse de forma suplementaria en la evolución de la ecuación de Schrödinger.
-Para una teoría de Broglie–Bohm en un espacio curvado con espín, el espacio de espín se convierte en un [[vector bundle] manojo de vectores] sobre el espacio de configuración y el potencial en la ecuación de Schrödinger en un operador local auto-adjunto actuando sobre tal espacio.<ref>Dürr, D., Goldstein, S., Taylor, J., Tumulka, R., and Zanghì, N., J. [http://arxiv.org/abs/quant-ph/0506173 "Quantum Mechanics in Multiply-Connected Spaces"], Phys. A: Math. Theor. 40, 2997&ndash;3031 (2007)</ref>
-===Teoría cuántica de campos===
-En Dürr et al.,<ref name="dgtz04">Dürr, D., Goldstein, S., Tumulka, R., and Zanghì, N., 2004, [http://arxiv.org/abs/quant-ph/0303156 "Bohmian Mechanics and Quantum Field Theory"], Phys. Rev. Lett. 93: 090402:1&ndash;4.</ref><ref>Dürr, D., Tumulka, R., and Zanghì, N., J. Phys. A: Math. Gen. 38, R1&ndash;R43 (2005), quant-ph/0407116</ref> los autores describen una extensión de la teoría de Broglie–Bohm para manejar operadores de creación y aniquilación. La idea básica es que tal espacio de configuración se convierte en el espacio (disjunto) de todas las posibles configuraciones de cualquier número de partículas- En lo que se refiere al tiempo, el sistema de desarrolla deterministicamente bajo la ecuación guía con un número fijo de partículas. Pero bajo un proceso estocástico, las partículas puden ser creadas y aniquiladas. La distribución de los eventos de creación es dictada por la función de onda. La función de onda misma evoluciona en todo momento sobre el espacio de configuración multi-partícula.
-Nikolic <ref name="nikolicqft">Nikolic, H. 2010 [http://arxiv.org/abs/0904.2287 "QFT as pilot-wave theory of particle creation and destruction"], Int. J. Mod. Phys. A 25, 1477 (2010)</ref> introduce una teoría de Broglie–Bohm puramente determinista de creación y destrucción, de acuerdo con la cuál las trayectorias de las partículas son continuas, pero los detectores de las partículas se comportan como si las partículas hubieran sido creadas o destruidas aunque una auténtica creación o destrucción de partículas nunca tenga lugar.
 == Referencia ==