Cuarto problema de Hilbert

En matemáticas, el cuarto problema de Hilbert (uno de los conocidos como veintitrés Problemas de Hilbert, publicados en 1900 por el matemático alemán David Hilbert) es una pregunta fundamental en geometría. En un enunciado derivado del original, el problema consiste en encontrar - descartando isomorfismos - todas las geometrías que tienen un sistema axiomático equivalente a los de la geometría clásica (es decir de la geometría euclídea, de la geometría hiperbólica y de la geometría elíptica), con aquellos axiomas de congruencia que involucran la desaparición del concepto de ángulo, y con la 'desigualdad triangular', considerada como un axioma, agregó.

Si se asume además el axioma de continuidad, entonces, en el caso del plano euclídeo, se llega al problema planteado por Darboux: "Determinar todos los problemas de cálculo de variaciones en el plano cuyas soluciones son todas las rectas del plano".​

Hay varias interpretaciones de la declaración original de Hilbert, pero sería el matemático alemán Georg Hamel el primero que contribuyó a la solución del cuarto problema de Hilbert.​

Una solución reconocida fue dada por el matemático ucraniano Alekséi Pogorélov en 1973.​​ En 1976, el matemático armenio Rouben V. Ambartzumian propuso otra prueba del cuarto problema de Hilbert.​

Declaración original

Hilbert analizó la existencia de geometrías no euclidianas y de geometrías no arquimedianas:

... una geometría en la que se cumplen todos los axiomas de la geometría euclidiana ordinaria y, en particular, todos los axiomas de congruencia excepto el de congruencia de triángulos (o todos excepto el teorema de la igualdad de los ángulos base en el triángulo isósceles), y en el que, además, se asume como axioma particular la proposición de que en todo triángulo la suma de dos lados es mayor que el tercero.​

Debido a la idea de que una 'línea recta' se define como el camino más corto entre dos puntos, mencionó cómo la congruencia de triángulos es necesaria para la prueba de Euclides de que una línea recta en el plano es la distancia más corta entre dos puntos. Lo resume de la forma siguiente:

El teorema de la línea recta como la distancia más corta entre dos puntos y el teorema esencialmente equivalente de Euclides sobre los lados de un triángulo, juegan un papel importante no solo en la teoría de números sino también en la teoría de superficies y en el cálculo de variaciones. Por esta razón, y porque creo que la investigación a fondo de las condiciones para la validez de este teorema arrojará una nueva luz sobre la idea de distancia, así como sobre otras ideas elementales, por ejemplo, sobre la idea del plano, y la posibilidad de su definición por medio de la idea de la línea recta, "la construcción y el tratamiento sistemático de las geometrías aquí posibles me parecen deseables".​

Métricas planas

Teorema de Desargues

Teorema de Desargues:

"Si dos triángulos se encuentran en un plano tal que las líneas que conectan los vértices correspondientes de los triángulos se encuentran en un punto, entonces los tres puntos, en los que las prolongaciones de los tres pares de lados correspondientes de los triángulos se cruzan, se encuentran en una línea recta".

La condición necesaria para resolver el cuarto problema de Hilbert es el requisito de que un espacio métrico que satisfaga los axiomas de este problema sea desarguesiano, es decir:

• si el espacio es de dimensión 2, entonces el teorema de Desargues y su inverso deben ser válidos;
• si el espacio tiene una dimensión mayor que 2, entonces cualesquiera tres puntos deben estar en un plano.

Para los espacios desarguesianos, Georg Hamel demostró que cada solución del cuarto problema de Hilbert se puede representar en un espacio proyectivo $RP^{n}$ real o en un dominio convexo de $RP^{n}$ si se determina la congruencia de los segmentos por la igualdad de sus longitudes en una métrica especial para la cual las líneas de la proyectiva del espacio son geodésicas.

Las métricas de este tipo se denominan planas o proyectivas.

Por tanto, la solución del cuarto problema de Hilbert se redujo a la solución del problema de la determinación constructiva de todas las métricas planas completas.

Hamel resolvió este problema bajo el supuesto de una alta regularidad de la métrica.​ Sin embargo, como muestran ejemplos simples, la clase de métricas planas regulares es más pequeña que la clase de todas las métricas planas. Los axiomas de las geometrías bajo consideración implican solo una continuidad de las métricas. Por lo tanto, para resolver completamente el cuarto problema de Hilbert es necesario determinar constructivamente todas las métricas planas continuas.

Prehistoria del cuarto problema de Hilbert

Modelo de Cayley-Klein de la geometría de Lobachevsky

Antes de 1900, se conocía el modelo de Cayley–Klein de la geometría de Lobachevsky en el disco unitario, según el que las líneas geodésicas son cuerdas del disco y la distancia entre puntos se define como un logaritmo de la razón anarmónica de una cuaterna de puntos. Para las métricas bidimensionales de Riemann, Eugenio Beltrami (1835-1900) demostró que las métricas planas son las métricas de curvatura constante.​

Para las métricas multidimensionales de Riemann, E. Cartan demostró esta afirmación en 1930.

En 1890, para resolver problemas sobre la teoría de los números, Hermann Minkowski introdujo una noción del espacio que hoy en día se llama espacio de Banach de dimensión finita.​

Espacio de Minkowski

Espacio de Minkowski

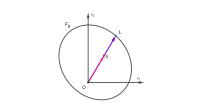
Sea $F_{0}\subset \mathbb {E} ^{n}$ una hipersuperficie convexa compacta en un espacio euclidiano definido por

$F_{0}=\{y\in E^{n}:F(y)=1\},$

donde la función $F=F(y)$ satisface las siguientes condiciones:

1. $F(y)\geqslant 0,\qquad F(y)=0\Leftrightarrow y=0;$
2. $F(\lambda y)=\lambda F(y),\qquad \lambda \geqslant 0;$
3. $F(y)\in C^{k}(E^{n}\setminus \{0\}),\qquad k\geqslant 3;$
4. y la fórmula ${\frac {\partial ^{2}F^{2}}{\partial y^{i}\,\partial y^{j}}}\xi ^{i}\xi ^{j}>0$ es definida positiva.

La longitud del vector OA está definida por:

$\|OA\|_{M}={\frac {\|OA\|_{\mathbb {E} }}{\|OL\|_{\mathbb {E} }}}.$

Un espacio con esta métrica se llama espacio de Minkowski.

La hipersuperficie $F_{0}$ es convexa y puede ser irregular. La métrica definida es plana.

Espacios de Finsler

Sean M y $TM=\{(x,y)|x\in M,y\in T_{x}M\}$ una variedad suave de dimensión finita y su paquete tangente, respectivamente. La función $F(x,y)\colon TM\rightarrow [0,+\infty )$ se llama métrica de Finsler si

1. $F(x,y)\in C^{k}(TM\setminus \{0\}),\qquad k\geqslant 3$;
2. Para cualquier punto $x\in M$, la restricción de $F(x,y)$ sobre $T_{x}M$ es la norma de Minkowski.

$(M,F)$ es el espacio de Finsler.

Geometría de Hilbert

Métrica de Hilbert

Sea $U\subset (\mathbb {E} ^{n+1},\|.\|_{\mathbb {E} })$ un conjunto convexo abierto acotado con el límite de clase C² y curvaturas normales positivas. De manera similar al espacio de Lobachevsky, la hipersuperficie $\partial U$ se llama el absoluto de la geometría de Hilbert.​

La distancia de Hilbert (véase la figura) está definida por

$d_{U}(p,q)={\frac {1}{2}}\ln {\frac {\|q-q_{1}\|_{E}}{\|q-p_{1}\|_{E}}}\times {\frac {\|p-p_{1}\|_{E}}{\|p-q_{1}\|_{E}}}.$

Métrica de Hilbert–Finsler

La distancia $d_{U}$ induce la métrica de Hilbert-Finsler $F_{U}$ en U. Para cualquier $x\in U$ y $y\in T_{x}U$ (véase la figura), se tiene que

$F_{U}(x,y)={\frac {1}{2}}\|y\|_{\mathbb {E} }\left({\frac {1}{\|x-x_{+}\|_{\mathbb {E} }}}+{\frac {1}{\|x-x_{-}\|_{\mathbb {E} }}}\right).$

La métrica es simétrica y plana. En 1895, Hilbert introdujo esta métrica como una generalización de la geometría de Lobachevsky. Si la hipersuperficie $\partial U$ es un elipsoide, entonces se tiene la geometría de Lobachevsky.

Métrica de Funk

En 1930, Funk introdujo una métrica no simétrica. Se define en un dominio delimitado por una hipersuperficie convexa cerrada y también es plana.

σ-métricas

Condición suficiente para métricas planas

Georg Hamel fue el primero en contribuir a la solución del cuarto problema de Hilbert.​ Probó la siguiente afirmación:

Teorema: Una métrica $F(x,y)=F(x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{n})$ de Finsler regular es plana si y solo si cumple la condición:

${\frac {\partial ^{2}F^{2}}{\partial x^{i}\,\partial y^{j}}}={\frac {\partial ^{2}F^{2}}{\partial x^{j}\,\partial y^{i}}},\,i,j=1,\ldots ,n.$

Fórmula de Crofton

Considérese un conjunto de todas las líneas rectas orientadas en un plano. Cada recta está definida por los parámetros $\rho$ y $\varphi ,$ donde $\rho$ es una distancia desde el origen a la recta, y $\varphi$ es un ángulo entre la recta y el eje x. Entonces, el conjunto de todas las líneas rectas orientadas es homeomorfo a un cilindro circular de radio 1 con el elemento de área $dS=d\rho \,d\varphi$. Sea $\gamma$ una curva rectificable en un plano. Entonces la longitud de $\gamma$ es

$L={\frac {1}{4}}\iint \limits _{\Omega }n(\rho ,\varphi )\,dp\,d\varphi$

donde $\Omega$ es un conjunto de líneas rectas que se cruzan con la curva $\gamma$ y $n(p,\varphi )$ es el número de intersecciones de la línea recta con $\gamma$. Crofton probó esta afirmación en 1870.​

Una declaración similar es válida para un espacio proyectivo.

Medida de Blaschke-Busemann

En 1966, en su charla en el Congreso Internacional de Matemáticos en Moscú, Herbert Busemann introdujo una nueva clase de métricas planas. Sobre un conjunto de líneas rectas en el plano proyectivo $RP^{2}$ introdujo una medida no negativa $\sigma$ completamente aditiva, que cumple las siguientes condiciones:

1. $\sigma (\tau P)=0$, donde $\tau P$ es un conjunto de líneas rectas que pasan por un punto P;
2. $\sigma (\tau X)>0$, donde $\tau X$ es un conjunto de líneas rectas que pasan a través de un conjunto X que contiene un segmento de línea recta;
3. $\sigma (RP^{n})$ es finita.

Si se considera una métrica $\sigma$ en un dominio convexo arbitrario $\Omega$ de un espacio proyectivo $RP^{2}$, entonces la condición 3) debe reemplazarse por lo siguiente: para cualquier conjunto H tal que H está contenido en $\Omega$ y el cierre de H no interseca el límite de $\Omega$, la desigualdad

$\sigma (\pi H)<\infty$ se mantiene.​

Usando esta medida, la métrica $\sigma$ en $RP^{2}$ está definida por

$|x,y|=\sigma \left(\tau [x,y]\right),$

donde $\tau [x,y]$ es el conjunto de líneas rectas que se cruzan con el segmento $[x,y]$.

La desigualdad del triángulo para esta métrica se deriva de teorema de Pasch.

Teorema: $\sigma$-métrica en $RP^{2}$ es plana, es decir, las geodésicas son las líneas rectas del espacio proyectivo.

Pero Busemann estaba lejos de la idea de que las métricas $\sigma$ agoten todas las métricas planas. Escribió: "La libertad en la elección de una métrica con geodésicas dadas es tan grande para las métricas no riemannianas que se puede dudar de si realmente existe una caracterización convincente de todos los espacios desarguesianos".​

Caja bidimensional

Teorema de Pogorelov

El siguiente teorema maravilloso fue probado por Pogorelov en 1973.​​

Teorema: Cualquier métrica plana completa continua bidimensional es una métrica $\sigma$.

Por tanto, el cuarto problema de Hilbert para el caso bidimensional quedó completamente resuelto.

Demostración de Ambartsumian

En 1976, Ambartsumian propuso otra prueba del cuarto problema de Hilbert.​

Su demostración utiliza el hecho de que en el caso bidimensional la medida completa puede ser restaurada por sus valores en biángulos y, por lo tanto, puede definirse en triángulos de la misma manera que el área de un triángulo se define en una esfera. Dado que la desigualdad del triángulo se cumple, se deduce que esta medida es positiva en los triángulos no degenerados y se determina en todos los conjuntos de Borel. Sin embargo, esta estructura no se puede generalizar a dimensiones superiores debido al tercer problema de Hilbert resuelto por Max Dehn.

En el caso bidimensional, los polígonos con el mismo volumen son oblicuamente congruentes. Como demostró Dehn, esto no es cierto para una dimensión superior.

Caja tridimensional

Para el caso tridimensional, Pogorelov demostró el siguiente teorema:

Teorema: Cualquier métrica plana completa regular tridimensional es una métrica $\sigma$.

Sin embargo, en el caso tridimensional, las medidas $\sigma$ pueden tomar valores positivos o negativos. Las condiciones necesarias y suficientes para que la métrica regular definida por la función del conjunto $\sigma$ sea plana son las siguientes tres condiciones:

1. el valor $\sigma$ en cualquier plano es igual a cero,
2. el valor $\sigma$ en cualquier cono no es negativo,
3. el valor $\sigma$ es positivo si el cono contiene puntos interiores.

Además, Pogorelov mostró que cualquier métrica plana continua completa en el caso tridimensional es el límite de las métricas $\sigma$ regulares con la convergencia uniforme en cualquier subdominio compacto del dominio de la métrica. Las llamó métricas $\sigma$ generalizadas.

Así, Pogorelov pudo probar la siguiente afirmación.

Teorema: En el caso tridimensional, cualquier métrica plana continua completa es una métrica $\sigma$ en sentido generalizado.

Busemann, en su reseña del libro de Pogorelov "El cuarto problema de Hilbert" escribió: "En el espíritu de la época, Hilbert se restringió a n = 2, 3 y también lo hace Pogorelov. Sin embargo, esto tiene sin duda razones pedagógicas, porque se dirige a una amplia clase de lectores. La verdadera diferencia está entre n = 2 y n > 2. El método de Pogorelov funciona para n > 3, pero requiere mayores tecnicismos".​

Caso multidimensional

El caso multidimensional del cuarto problema de Hilbert fue estudiado por Szabo.​ En 1986, demostró, como escribió, el teorema de Pogorelov generalizado.

Teorema: Cada espacio n-dimensional desarguesiano de la clase $C^{n+2},n>2$, es generado por la construcción de Blaschke–Buzeman.

Una $\sigma$-medida que genera una medida plana tiene las siguientes propiedades:

1. la medida $\sigma$ de los hiperplanos que pasan por un punto fijo es igual a cero;
2. la medida $\sigma$ del conjunto de hiperplanos que cruzan dos segmentos [x, y], [y, z], donde x, y та z no son colineales, es positivo.

Se dio el ejemplo de una métrica plana no generada por la construcción de Blaschke-Busemann. Szabo describió todas las métricas planas continuas en términos de funciones generalizadas.

Cuarto problema de Hilbert y cuerpos convexos

El cuarto problema de Hilbert también está estrechamente relacionado con las propiedades de los cuerpos convexos. Un poliedro convexo se llama zonotopo si es la suma de Minkowski de segmentos. Un cuerpo convexo que es un límite de zonotopos en la métrica de Blaschke-Hausdorff se llama zonoide. Para los zonoides, la función de soporte está representada por

$h(x)=\int \limits _{S^{n-1}}|\langle x,u\rangle |\,\partial \sigma (u),\qquad (1)$

donde $\sigma (u)$ es una medida de Borel incluso positiva en una esfera $S^{n-1}$.

El espacio de Minkowski es generado por la construcción de Blaschke-Busemann si y solo si la función de soporte de la indicatriz tiene la forma de (1), donde $\sigma (u)$ es par y no necesariamente con medida de Borel positiva.​ Los cuerpos delimitados por tales hipersuperficies se denominan zonoides generalizados.

El octaedro $|x_{1}|+|x_{2}|+|x_{3}|\leqslant 1$ en el espacio euclídeo $E^{3}$ no es un zonoide generalizado. De la declaración anterior se deduce que la métrica plana del espacio de Minkowski con la norma $\|x\|=\max\{|x_{1}|,|x_{2}|,|x_{3}|\}$ no es generada por la construcción de Blaschke-Busemann.

Generalizaciones del cuarto problema de Hilbert

Se encontró la correspondencia entre las métricas planas n dimensionales de Finsler y las formas simplécticas especiales en la variedad de Grassmann $G(n+1,2)$ × $E^{n+1}$.​

Se consideraron soluciones periódicas del cuarto problema de Hilbert:

1) Sea (M, g) una variedad compacta localmente euclídea de Riemann. Supóngase que se da la métrica de Finsler $C^{2}$ en M con las mismas geodésicas que en la métrica g. Entonces, la métrica de Finsler es la suma de una métrica local de Minkovski y una forma 1 cerrada.​

2) Sea (M, g) un espacio compacto simétrico de Riemann de rango mayor que uno. Si F es una métrica de Finsler $C^{2}$ simétrica cuyas geodésicas coinciden con las geodésicas de la métrica de Riemann g, entonces (M, g) es un espacio de Finsler simétrico.​ El análogo de este teorema para espacios simétricos de rango uno aún no se ha probado.

Otra exposición del cuarto problema de Hilbetrt se puede encontrar en la obra de Paiva.​

Problemas no resueltos

1. El cuarto problema de Hilbetrt para la métrica de Finsler no simétrica aún no se ha resuelto.
2. No se ha proporcionado la descripción de la métrica en $RP^{n}$ para la cual los k-planos minimizan el k-área (Busemann).​

Lecturas relacionadas

• Busemann, Herbert (1976). «Problem IV. Desarguesian spaces». En Browder, Felix E., ed. Mathematical Developments Arising from Hilbert Problems. American Mathematical Society XXVIII. American Mathematical Society. pp. 131-141. ISBN 0-8218-1428-1. Zbl 0352.50010. 
• Papadopoulos, Athanase (2014). «Hilbert's fourth problem». Handbook of Hilbert geometry (A. Papadopoulos and M. Troyanov, ed.). IRMA Lectures in Mathematics and Theoretical Physics 22. European Mathematical Society. pp. 391-432. ISBN 978-3-03719-147-7. 

• Datos: Q4515035