Explicaciones mecánicas de la gravitación

Las explicaciones mecánicas de la gravitación (o teorías cinéticas de la gravitación) son intentos de explicar la acción de la gravedad con la ayuda de procesos mecánicos básicos, como fuerzas de presión causadas por impulsos, sin el uso de ninguna acción a distancia. Estas teorías se desarrollaron desde el siglo XVI hasta el siglo XIX en relación con el éter. Sin embargo, estos modelos ya no se consideran teorías viables dentro de la comunidad científica dominante y la relatividad general es ahora el modelo estándar para describir la gravitación sin el uso de acciones a distancia. Las hipótesis modernas de "gravedad cuántica" también intentan describir la gravedad mediante procesos más fundamentales, como los campos de partículas, pero no se basan en la mecánica clásica.

Emisiones

Esta teoría es probablemente​ la explicación mecánica más conocida, y fue desarrollada por primera vez por Nicolas Fatio de Duillier en 1690, y reinventada, entre otros, por Georges-Louis Le Sage (1748), Lord Kelvin (1872) y Hendrik Lorentz (1900), y criticada por James Clerk Maxwell (1875) y Henri Poincaré (1908).

La teoría postula que la fuerza de gravedad es el resultado de pequeñas partículas u ondas que se mueven a gran velocidad en todas direcciones, a lo largo del universo. Se supone que la intensidad del flujo de partículas es la misma en todas las direcciones, por lo que un objeto aislado A es golpeado por igual desde todos los lados, lo que genera solo una presión dirigida hacia adentro pero ninguna fuerza direccional neta. Sin embargo, si hay un segundo objeto B presente, una fracción de las partículas que de otro modo habrían golpeado a A desde la dirección de B se intercepta, de modo que B funciona como un escudo, por así decirlo, es decir, desde la dirección de B, A será golpeado por menos partículas que desde la dirección opuesta. De la misma manera, B será golpeado por menos partículas desde la dirección de A que desde la dirección opuesta. Se puede decir que A y B se "hacen sombra" mutuamente y que los dos cuerpos son empujados uno hacia el otro por el desequilibrio de fuerzas resultante.

P5: Permeabilidad, atenuación y proporcionalidad de masa

Esta sombra obedece a la ley de la inversa del cuadrado, porque el desequilibrio del flujo de momento sobre toda una superficie esférica que encierra el objeto es independiente del tamaño de la esfera que la encierra, mientras que el área de la superficie de la esfera aumenta en proporción al cuadrado del radio. Para satisfacer la necesidad de proporcionalidad de masa, la teoría postula que a) los elementos básicos de la materia son muy pequeños, de modo que la materia bruta consiste principalmente de espacio vacío, y b) que las partículas son tan pequeñas que solo una pequeña fracción de ellas sería interceptada por la materia bruta. El resultado es que la "sombra" de cada cuerpo es proporcional a la superficie de cada elemento de materia.

Crítica: Esta teoría fue rechazada principalmente por razones termodinámicas porque en este modelo solo aparece una sombra si las partículas u ondas son absorbidas al menos parcialmente, lo que debería provocar un enorme calentamiento de los cuerpos. Además, la resistencia, es decir, la resistencia de las corrientes de partículas en la dirección del movimiento, también es un gran problema. Este problema se puede resolver suponiendo velocidades superlumínicas, pero esta solución aumenta en gran medida los problemas térmicos y contradice la relatividad especial.​​

Vórtices

Vórtices de éter alrededor de los cuerpos celestes

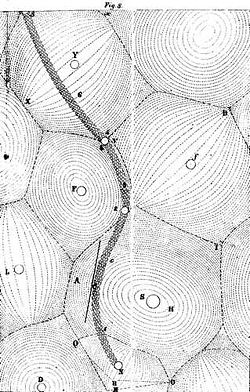
Debido a sus creencias filosóficas, René Descartes propuso en 1644 que no puede existir ningún espacio vacío y que, en consecuencia, el espacio debe estar lleno de materia. Las partes de esta materia tienden a moverse en trayectorias rectas, pero como están próximas entre sí, no pueden moverse libremente, lo que según Descartes implica que todo movimiento es circular, por lo que el éter está lleno de vórtices. Descartes también distingue entre diferentes formas y tamaños de materia en las que la materia rugosa resiste más fuertemente el movimiento circular que la materia fina. Debido a la fuerza centrífuga, la materia tiende hacia los bordes exteriores del vórtice, lo que provoca una condensación de esta materia allí. La materia rugosa no puede seguir este movimiento debido a su mayor inercia, por lo que debido a la presión de la materia exterior condensada, esas partes serán empujadas hacia el centro del vórtice. Según Descartes, esta presión interna no es otra cosa que la gravedad. Comparó este mecanismo con el hecho de que si se detiene un recipiente giratorio lleno de líquido, el líquido continúa girando. Ahora bien, si se dejan caer pequeños trozos de materia ligera (por ejemplo, madera) en el recipiente, los trozos se mueven hacia el centro del recipiente.​​​ Esta idea sobre la formación del cosmos por vórtices de materia fue precedida por los antiguos atomistas presocráticos Leucipo y Demócrito.​

Siguiendo las premisas básicas de Descartes, Christiaan Huygens diseñó entre 1669 y 1690 un modelo de vórtice mucho más exacto. Este modelo fue la primera teoría de la gravitación que se elaboró matemáticamente. Supuso que las partículas de éter se movían en todas direcciones, pero eran arrojadas hacia los bordes exteriores del vórtice y esto causaba (como en el caso de Descartes) una mayor concentración de materia fina en los bordes exteriores. También en su modelo la materia fina presiona a la materia rugosa hacia el centro del vórtice. Huygens también descubrió que la fuerza centrífuga es igual a la fuerza que actúa en dirección al centro del vórtice (fuerza centrípeta). También postuló que los cuerpos deben consistir principalmente en espacio vacío para que el éter pueda penetrarlos fácilmente, lo cual es necesario para la proporcionalidad de la masa. Concluyó además que el éter se mueve mucho más rápido que los cuerpos que caen. En esta época, Newton desarrolló su teoría de la gravitación que se basa en la atracción, y aunque Huygens coincidía con el formalismo matemático, decía que el modelo era insuficiente debido a la falta de una explicación mecánica de la ley de fuerza. El descubrimiento de Newton de que la gravedad obedece a la ley del cuadrado inverso sorprendió a Huygens y trató de tenerlo en cuenta asumiendo que la velocidad del éter es menor a mayor distancia.​​​

Crítica: Newton se opuso a la teoría porque la resistencia debía provocar desviaciones notables de las órbitas que no se observaban.​ Otro problema era que las lunas a menudo se movían en direcciones diferentes, contra la dirección del movimiento del vórtice. Además, la explicación de Huygens de la ley del cuadrado inverso es circular, porque esto significa que el éter obedece la tercera ley de Kepler. Pero una teoría de la gravitación tiene que explicar esas leyes y no debe presuponerlas.​​

Varios físicos británicos desarrollaron la teoría del vórtice del átomo a finales del siglo XIX. Sin embargo, el físico William Thomson, primer barón Kelvin, desarrolló un enfoque bastante distinto. Mientras que Descartes había esbozado tres especies de materia, cada una vinculada respectivamente a la emisión, transmisión y reflexión de la luz, Thomson desarrolló una teoría basada en un continuo unitario.​

Flujos

En una carta de 1675 a Henry Oldenburg, y más tarde a Robert Boyle, Newton escribió lo siguiente: [La gravedad es el resultado de] “una condensación que causa un flujo de éter con un adelgazamiento correspondiente de la densidad del éter asociada con la mayor velocidad del flujo”. También afirmó que tal proceso era consistente con todos sus otros trabajos y las Leyes del movimiento de Kepler.​ La idea de Newton de una caída de presión asociada con una mayor velocidad de flujo se formalizó matemáticamente como el principio de Bernoulli publicado en el libro Hydrodynamica de Daniel Bernoulli en 1738.

Sin embargo, aunque más tarde propuso una segunda explicación (véase la sección siguiente), los comentarios de Newton a esa pregunta siguieron siendo ambiguos. En la tercera carta a Bentley en 1692 escribió:​

Es inconcebible que la materia bruta inanimada pueda, sin la mediación de algo más que no sea material, operar sobre otra materia y afectarla, sin contacto mutuo, como debe hacerlo si la gravitación en el sentido de Epicuro es esencial e inherente a ella. Y ésta es una de las razones por las que deseaba que no me atribuyeras una «gravedad innata». Que la gravedad sea innata, inherente y esencial a la materia, de modo que un cuerpo pueda actuar sobre otro a distancia, a través del vacío, sin la mediación de nada más, por medio de lo cual su acción y fuerza puedan transmitirse de uno a otro, es para mí un absurdo tan grande que creo que ningún hombre que tenga una facultad competente de pensamiento en cuestiones filosóficas puede caer jamás en él. La gravedad debe ser causada por un agente que actúa constantemente según ciertas leyes; pero el que este agente sea material o inmaterial lo he dejado a la consideración de mis lectores.

Por otra parte, Newton también es conocido por la frase Hypotheses non fingo, escrita en 1713:​

Todavía no he podido descubrir la razón de estas propiedades de la gravedad a partir de los fenómenos, y no hago hipótesis. Porque todo lo que no se deduce de los fenómenos debe llamarse hipótesis; y las hipótesis, ya sean metafísicas o físicas, o basadas en cualidades ocultas, o mecánicas, no tienen cabida en la filosofía experimental. En esta filosofía se infieren proposiciones particulares de los fenómenos y luego se vuelven generales por inducción.

Y según el testimonio de algunos de sus amigos, como Nicolas Fatio de Duillier o David Gregory, Newton pensaba que la gravitación se basa directamente en la influencia divina.​

Similar a Newton, pero matemáticamente con mayor detalle, Bernhard Riemann asumió en 1853 que el éter gravitacional es un fluido incompresible y que la materia normal representa sumideros en este éter. De modo que si el éter se destruye o se absorbe proporcionalmente a las masas dentro de los cuerpos, surge una corriente que arrastra a todos los cuerpos circundantes en dirección a la masa central. Riemann especuló que el éter absorbido se transfiere a otro mundo o dimensión.​

Otro intento de resolver el problema energético fue realizado por Iván Yarkovski en 1888. Basándose en su modelo de corriente de éter, que era similar al de Riemann, argumentó que el éter absorbido podría convertirse en nueva materia, lo que llevaría a un aumento de la masa de los cuerpos celestes.​

Crítica: Como en el caso de la teoría de Le Sage, la desaparición de energía sin explicación viola la ley de conservación de la energía. También debe surgir algún arrastre, y no se conoce ningún proceso que conduzca a la creación de materia.

Presión estática

Newton actualizó la segunda edición de Óptica (1717) con otra teoría mecánico-etérica de la gravedad. A diferencia de su primera explicación (1675 – ver Corrientes), propuso un éter estacionario que se vuelve cada vez más delgado cerca de los cuerpos celestes. Por analogía con la sustentación, surge una fuerza que empuja todos los cuerpos hacia la masa central. Minimizó la resistencia al afirmar una densidad extremadamente baja del éter gravitacional.

Al igual que Newton, Leonhard Euler presupuso en 1760 que el éter gravitacional pierde densidad de acuerdo con la ley del cuadrado inverso. De manera similar a otros, Euler también asumió que, para mantener la proporcionalidad de la masa, la materia consiste principalmente de espacio vacío.​

Crítica: Tanto Newton como Euler no dieron ninguna razón por la cual la densidad de ese éter estático debería cambiar. Además, James Clerk Maxwell señaló que en este "hidrostático" modelo "el estado de tensión... que debemos suponer que existe en el medio invisible, es 3000 veces mayor que el que el acero más fuerte podría soportar".​

Ondas

Robert Hooke especuló en 1671 que la gravitación es el resultado de que todos los cuerpos emiten ondas en todas las direcciones a través del éter. Otros cuerpos, que interactúan con estas ondas, se mueven en la dirección de la fuente de las ondas. Hooke vio una analogía con el hecho de que pequeños objetos en una superficie de agua perturbada se mueven hacia el centro de la perturbación.​

James Challis elaboró matemáticamente una teoría similar entre 1859 y 1876. Calculó que el caso de atracción ocurre si la longitud de onda es grande en comparación con la distancia entre los cuerpos gravitacionales. Si la longitud de onda es pequeña, los cuerpos se repelen entre sí. Mediante una combinación de estos efectos, también intentó explicar todas las demás fuerzas.​

Crítica: Maxwell objetó que esta teoría requiere una producción constante de ondas, que debe ir acompañada de un consumo infinito de energía.​ El propio Challis admitió que no había llegado a un resultado definitivo debido a la complejidad de los procesos.​

Pulsaciones

Lord Kelvin (1871) y Carl Anton Bjerknes (1871) asumieron que todos los cuerpos pulsan en el éter. Esto era análogo al hecho de que, si la pulsación de dos esferas en un fluido está en fase, se atraerán entre sí; y si la pulsación de dos esferas no está en fase, se repelerán entre sí. Este mecanismo también se utilizó para explicar la naturaleza de las cargas eléctricas. Esta hipótesis también ha sido examinada, entre otros, por George Gabriel Stokes y Woldemar Voigt.​

Crítica: Para explicar la gravitación universal, uno se ve obligado a suponer que todas las pulsaciones del universo están en fase, lo que parece muy inverosímil. Además, el éter debe ser incompresible para garantizar que la atracción también surja a distancias mayores.​ Y Maxwell argumentó que este proceso debe ir acompañado de una nueva producción y destrucción permanente de éter.​

Otras especulaciones históricas

En 1690, Pierre Varignon asumió que todos los cuerpos están expuestos a empujes de partículas de éter desde todas las direcciones y que existe algún tipo de limitación a cierta distancia de la superficie de la Tierra que las partículas no pueden atravesar. Supuso que si un cuerpo está más cerca de la Tierra que del límite de limitación, entonces el cuerpo experimentaría un mayor empuje desde arriba que desde abajo, provocando que cayera hacia la Tierra.​

En 1748, Mijaíl Lomonósov supuso que el efecto del éter es proporcional a la superficie completa de los componentes elementales que forman la materia (similar a Huygens y Fatio antes que él). Supuso también una enorme penetrabilidad de los cuerpos. Sin embargo, no dio ninguna descripción clara de cómo exactamente el éter interactúa con la materia para que surja la ley de la gravitación.​

En 1821, John Herapath intentó aplicar su modelo co-desarrollado de la teoría cinética de los gases sobre la gravitación. Supuso que el éter es calentado por los cuerpos y pierde densidad, de modo que otros cuerpos son empujados a estas regiones de menor densidad.​ Sin embargo, Taylor demostró que la disminución de la densidad debida a la expansión térmica se compensa con la mayor velocidad de las partículas calentadas; por lo tanto, no surge atracción.​

Teorización reciente

Estas explicaciones mecánicas de la gravedad nunca obtuvieron una aceptación generalizada, aunque los físicos siguieron estudiándolas ocasionalmente hasta principios del siglo XX, momento en el que se consideraban generalmente desacreditadas. Sin embargo, algunos investigadores fuera de la corriente científica dominante todavía intentan descubrir algunas consecuencias de esas teorías.

La teoría de Le Sage fue estudiada por Radzievskii y Kagalnikova (1960),​ Shneiderov (1961),​ Buonomano y Engels (1976),​ Adamut (1982),​ y Edwards (2014).​

La gravedad debida a la presión estática fue estudiada recientemente por Arminjon.​​

Véase también

• Historia de la teoría de la gravitación
• Teoría de la gravitación de Le Sage

Fuentes

• Aiton, E.J. (1969), «Newton's Aether-Stream Hypothesis and the Inverse Square Law of Gravitation», Annals of Science 25 (3): 255-260, doi:10.1080/00033796900200151 .

• Carrington, Hereward (1913), «Earlier Theories of Gravity», en Sugden, Sherwood J. B, ed., The Monist 23 (3): 445-458, doi:10.5840/monist19132332 .

• Drude, Paul (1897), «Ueber Fernewirkungen», Annalen der Physik 298 (12): I-XLIX, Bibcode:1897AnP...298D...1D, doi:10.1002/andp.18972981220 .

• Hall, Thomas Proctor (1895), «Physical Theories of Gravitation», Proceedings of the Iowa Academy of Science 3: 47-52 .

• Helm, Georg (1881), «Ueber die Vermittelung der Fernewirkungen durch den Aether», Annalen der Physik 250 (9): 149-176, Bibcode:1881AnP...250..149H, doi:10.1002/andp.18812500912 .

• Isenkrahe, Caspar (1892), «Über die Rückführung der Schwere auf Absorption und die daraus abgeleiteten Gesetze», Abhandlungen zur Geschichte der Mathematik 6, Leipzig, pp. 161-204 .

• Maxwell, James Clerk (1878), "Atom" , in Baynes, T. S. (ed.), Encyclopædia Britannica, vol. 3 (9th ed.), New York: Charles Scribner's Sons, pp. 36–49
• Maxwell, James Clerk (1878), "Attraction" , in Baynes, T. S. (ed.), Encyclopædia Britannica, vol. 3 (9th ed.), New York: Charles Scribner's Sons, pp. 63–65
• Peck, J. W. (1903), «The Corpuscular Theories of Gravitation», Proceedings of the Royal Philosophical Society of Glasgow 34: 17-44 .

• Poincaré, Henri (1914) [1908], «Lesage's theory», Science and Method, London, New York: Nelson & Sons, pp. 246-253 .

• Preston, Samuel Tolver (1895), «Comparative Review of some Dynamical Theories of Gravitation», Philosophical Magazine, 5th series 39 (237): 145-159, doi:10.1080/14786449508620698 .

• Taylor, William Bower (1876), «Kinetic Theories of Gravitation», Smithsonian Report: 205-282 .

• Van Lunteren, F. (2002), «Nicolas Fatio de Duillier on the mechanical cause of Gravitation», en Edwards, M.R., ed., Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation, Montreal: C. Roy Keys Inc., pp. 41-59 .

• Zehe, Horst (1980), «Die Gravitationstheorie des Nicolas Fatio de Duillier», Archive for History of Exact Sciences (Hildesheim: Gerstenberg) 28 (1): 1-23, Bibcode:1983AHES...28....1Z, ISBN 3-8067-0862-2, S2CID 123509380, doi:10.1007/BF00327787 .

• Zenneck, Jonathan (1903), «Gravitation», Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen 5 (1), pp. 25-67, ISBN 978-3-663-15445-7, doi:10.1007/978-3-663-16016-8_2 . (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).

Enlaces externos

• • Datos: Q1915536