Hipotrocoide

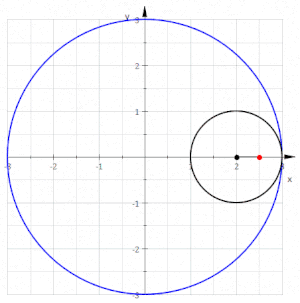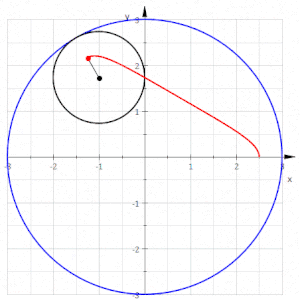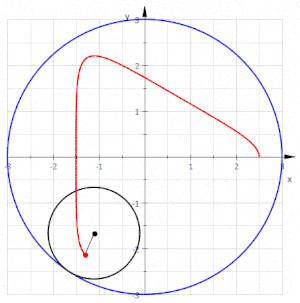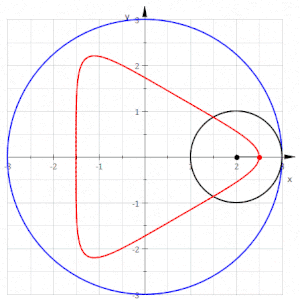
Una hipotrocoide, en geometría, es la curva plana que describe un punto vinculado a una circunferencia generatriz que rueda dentro de una circunferencia directriz, tangencialmente, sin deslizamiento.

La palabra se compone de las raíces griegas hipo hupo (abajo) y trokos (rueda).

Estas curvas fueron estudiadas por Albrecht Dürer en 1525, Ole Christensen Rømer en 1674 y Bernoulli en 1725.

Ecuaciones

Siendo $q={\dfrac {a}{b}}$ (donde $q>1$ ) y $d=kb$ , con circunferencia directriz de radio a, y circunferencia generatriz de radio a, y la distancia al centro de la generatriz d, la ecuación de la hipotrocoide es:

z=a=x

pero x no es igual a A

donde:

qz=a[(q-1)e^{it}+ke^{-i(q-1)t}]\,

q(x+iy)=a(q-1)\cos(t)+ia(q-1)\sin(t)+ak\cos[(q-1)t]-iak\sin[(q-1)t]

Por identificación de las partes reales e imaginarias se obtiene:

qx=a(q-1)\cos(t)+ka\cos[(q-1)t)];\,

qy=a(q-1)\sin(t)-ka\sin[(q-1)t)];\,

donde:

q={\dfrac {a}{b}}

y

k={\dfrac {d}{b}}\,

.

Sabiendo que $a=R$ , $b=r$ y $t=\theta$ , obtenemos las ecuaciones siguientes:

x=(R-r)\cos \theta +d\cos \left({R-r \over r}\theta \right)

y=(R-r)\sin \theta -d\sin \left({R-r \over r}\theta \right)

el ángulo $\theta$ varía de 0 a 2π.

Las elipses son casos particulares de hipotrocoide, donde $R=2r$ .

Las hipocicloides son casos particulares, donde $d=r$ (el punto fijo de la generatriz)

Hipotrocoide alargada (en trazo rojo), circunferencia directriz (en trazo azul), circunferencia generatriz (en trazo negro). Parámetros: R = 3, r = 1, d = 1,5).

Hipotrocoide acortada (en trazo rojo), circunferencia directriz (en trazo azul), circunferencia generatriz (en trazo negro). Parámetros: R = 3, r = 1, d = 0,5.

Aplicaciones

Los espirografos (son juguetes para dibujar) crean hipotrocoides.
Las hipotrocoides definen el soporte de los autovalores de matrices aleatorias con correlaciones cíclicas.^[1]

Curvas cíclicas

Curva cíclica

La directriz es una recta
d = r	d < r	d > r
cicloide	trocoide
cicloide normal	cicloide acortada	cicloide alargada

La directriz es una circunferencia
	d = r	d < r	d > r
La generatriz es exterior a al directriz	epicicloide	epitrocoide
	epicicloide normal	epicicloide acortada	epicicloide alargada
La generatriz es interior a al directriz	hipocicloide	hipotrocoide
	hipocicloide normal	hipocicloide acortada	hipocicloide alargada
La directriz es interior a al generatriz	pericicloide	peritrocoide
	pericicloide normal	pericicloide acortada	pericicloide alargada