Método del medio del cuadrado

Una iteración del método del medio del cuadrado, que muestra una semilla de 6 dígitos, que luego se eleva al cuadrado y el valor resultante tiene sus 6 dígitos del medio como valor de salida (y también como la siguiente semilla para la secuencia)

En matemáticas y en informática, el método del medio del cuadrado (en ocasiones traducido del término original en inglés middle-square method como método del cuadrado medio) es un método para generar números pseudoaleatorios. En la práctica, es un método inadecuado para muchos propósitos, ya que su periodo suele ser muy corto y tiene algunas debilidades graves. Así, si se itera el número suficiente de veces, el método del cuadrado medio comenzará a generar repetidamente el mismo número o volverá a un número anterior en la secuencia y repetirá el ciclo indefinidamente.

Historia

En matemáticas

Grafo dirigido de los 100 números pseudoaleatorios de 2 dígitos obtenidos mediante el método del medio del cuadrado con n = 2

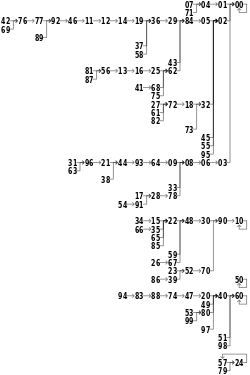
El método fue inventado por John von Neumann y lo describió en una conferencia en 1949.​

En su conferencia de 1949, Von Neumann bromeó diciendo que cualquiera que considere métodos aritméticos para producir dígitos aleatorios está, por supuesto, en un estado de pecado. Lo que quería decir, explicó, era que no había verdaderos números aleatorios, solo medios para producirlos, y un procedimiento aritmético estricto, como el método del medio del cuadrado, no es un método de ese tipo. Sin embargo, descubrió que estos métodos eran cientos de veces más rápidos que leer números verdaderamente aleatorios procedentes de listas almacenadas en tarjetas perforadas, lo que tenía importancia práctica para su trabajo de programación sobre el ordenador ENIAC. Encontró que la destrucción de secuencias de medios de cuadrados era un factor a su favor, porque podía detectarse fácilmente: uno siempre teme la aparición de ciclos cortos no detectados.​ Nicholas Metropolis informó secuencias de 750.000 dígitos antes de la destrucción mediante el uso de números de 38 bits con el método del medio del cuadrado.​

El libro "The Broken Dice" de Ivar Ekeland ofrece un relato extenso de cómo un fraile franciscano conocido simplemente como el hermano Edvin inventó el método en algún momento entre 1240 y 1250.​ Supuestamente, el manuscrito está perdido, pero Jorge Luis Borges le envió a Ekeland una copia que hizo en la Biblioteca del Vaticano.

La modificación del algoritmo del cuadrado medio con una serie de Weyl mejora el período y la aleatoriedad.​​

El método

Para generar una secuencia de números pseudoaleatorios de n dígitos, se crea un valor inicial de n dígitos y se eleva al cuadrado, lo que produce un número de 2 n dígitos. Si el resultado tiene menos de 2 n dígitos, se agregan ceros a la izquierda hasta obtener el número de dígitos prefijado. Los n dígitos del medio (los situados en las n posiciones centrales) del resultado serían el siguiente número en la secuencia y se devolverían como resultado. El proceso se repite a continuación para generar más números.

El valor de n debe ser par para que el método funcione: si el valor de n es impar, entonces no necesariamente habrá n dígitos centrales definidos de forma única para seleccionar. Considérese lo siguiente: si se eleva al cuadrado un número de 3 dígitos, puede producir un número de 6 dígitos (p. ej. 540² = 291600). Si hubiera 3 dígitos centrales, eso dejaría 6 - 3 = 3 dígitos para distribuir a la izquierda y derecha del medio. Pero es imposible distribuir uniformemente estos dígitos de manera igualitaria en ambos lados del número central y, por lo tanto, no hay "dígitos centrales". Es aceptable rellenar las semillas con ceros a la izquierda para crear un número de n dígitos de valor par (por ejemplo, 540 → 0540).

En el caso de un generador de números de n dígitos, el período no puede ser mayor que 8ⁿ. Si los n dígitos del medio son todos ceros, el generador generará ceros indefinidamente. Si la primera mitad de un número en la secuencia son ceros, los números subsiguientes serán decrecientes hasta cero. Si bien estas series de ceros son fáciles de detectar, ocurren con demasiada frecuencia para que este método sea de uso práctico. El método del cuadrado medio también puede quedarse atascado en un número distinto de cero. Para n = 4, esto ocurre con los valores 0100, 2500, 3792 y 7600. Otros valores de la semilla forman ciclos repetitivos muy cortos, como por ejemplo 0540 → 2916 → 5030 → 3009. Estos fenómenos son aún más obvios cuando n = 2, ya que ninguna de las 100 semillas posibles genera más de 14 iteraciones sin volver a 0, 10, 50, 60 o a un bucle como 24 → 57.

Ejemplo de código

Aquí, el algoritmo se representa en Python 3.12.

seed_number= int(input("Please enter a four-digit number:\n[####] "))
number= seed_number
already_seen= set()
counter= 0

while number not in already_seen:
    counter += 1
    already_seen.add(number)
    number= int(str(number * number).zfill(8)[2:6])  # zfill adds padding of zeroes
    print(f"#{counter}: {number}")

print(f"We began with {seed_number} and"
      f" have repeated ourselves after {counter} steps"
      f" with {number}.")

Véase también

• Generador lineal congruencial
• Blum Blum Shub
• Función hash

Referencias

• Datos: Q466575