matemáticas , la sustitución trigonométrica consiste en la sustitución de determinadas expresiones mediante el uso de funciones trigonométricas . En cálculo , la sustitución trigonométrica es una técnica que permite evaluar integrales, puesto que se pueden utilizar identidades trigonométricas para simplificar ciertas integrales que contienen expresiones radicales .[ 1] [ 2]
a
2
−
x
2
{\displaystyle a^{2}-x^{2}}
[ editar ]
Se hace el cambio de variable
x
=
a
sen
θ
{\displaystyle x=a\operatorname {sen} \theta }
identidad trigonométrica
sen
2
(
θ
)
+
cos
2
(
θ
)
=
1
{\displaystyle \operatorname {sen} ^{2}(\theta )+\cos ^{2}(\theta )=1}
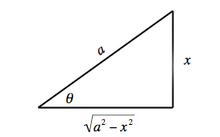
Construcción geométrica para Caso
I
{\displaystyle {\text{I}}}
Para calcular la integral
∫
d
x
a
2
−
x
2
{\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}}
se puede realizar el cambio de variable
x
=
a
sen
θ
d
x
=
a
cos
θ
d
θ
θ
=
arcsen
(
x
a
)
{\displaystyle {\begin{aligned}x&=a\operatorname {sen} \theta \\dx&=a\cos \theta \;d\theta \\\theta &={\text{arcsen}}\left({\frac {x}{a}}\right)\end{aligned}}}
entonces
∫
d
x
a
2
−
x
2
=
∫
a
cos
θ
a
2
−
a
2
sen
2
θ
d
θ
=
∫
a
cos
θ
a
2
(
1
−
sen
2
θ
)
d
θ
=
∫
a
cos
θ
a
2
cos
2
θ
d
θ
=
∫
d
θ
=
θ
+
C
=
arcsen
(
x
a
)
+
C
{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta }{\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\;d\theta \\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&={\text{arcsen}}\left({\frac {x}{a}}\right)+C\end{aligned}}}
Los pasos anteriores requirieron que
a
>
0
{\displaystyle a>0}
cos
θ
>
0
{\displaystyle \cos \theta >0}
Es posible escoger
a
{\displaystyle a}
a
2
{\displaystyle a^{2}}
−
π
/
2
<
θ
<
π
/
2
{\displaystyle -\pi /2<\theta <\pi /2}
arco seno .
Para una integral definida, se debe averiguar cómo cambian los límites de la integración. Por ejemplo, cuando
x
{\displaystyle x}
0
{\displaystyle 0}
a
/
2
{\displaystyle a/2}
sen
θ
{\displaystyle \operatorname {sen} \theta }
0
{\displaystyle 0}
1
/
2
{\displaystyle 1/2}
θ
{\displaystyle \theta }
0
{\displaystyle 0}
π
/
6
{\displaystyle \pi /6}
∫
0
a
/
2
d
x
a
2
−
x
2
=
∫
0
π
/
6
d
θ
=
π
6
.
{\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.}
Se necesita elegir los límites con cuidado. Debido a que la integración anterior requiere que
−
π
/
2
<
θ
<
π
/
2
{\displaystyle -\pi /2<\theta <\pi /2}
θ
{\displaystyle \theta }
0
{\displaystyle 0}
π
/
6
{\displaystyle \pi /6}
θ
{\displaystyle \theta }
π
{\displaystyle \pi }
5
π
/
6
{\displaystyle 5\pi /6}
Alternativamente, se deben evaluar completamente las integrales indefinidas antes de aplicar las condiciones de contorno. En ese caso, la antiderivada da
∫
0
a
/
2
d
x
a
2
−
x
2
=
arcsen
(
x
a
)
|
0
a
/
2
=
arcsen
(
1
2
)
−
arcsen
(
0
)
=
π
6
{\displaystyle {\begin{aligned}\int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\operatorname {arcsen} \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}\\&=\operatorname {arcsen} \left({\frac {1}{2}}\right)-\operatorname {arcsen} (0)\\&={\frac {\pi }{6}}\end{aligned}}}
como antes.
La integral
∫
a
2
−
x
2
d
x
{\displaystyle \int {\sqrt {a^{2}-x^{2}}}\,dx}
puede ser evaluada haciendo el cambio de variable
x
=
a
sen
θ
d
x
=
a
cos
θ
d
θ
θ
=
arcsen
(
x
a
)
{\displaystyle {\begin{aligned}x&=a\operatorname {sen} \theta \\dx&=a\cos \theta \;d\theta \\\theta &={\text{arcsen}}\left({\frac {x}{a}}\right)\end{aligned}}}
donde
a
>
0
{\displaystyle a>0}
a
2
=
a
{\displaystyle {\sqrt {a^{2}}}=a}
−
π
2
≤
θ
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}}
porque
cos
θ
≥
0
{\displaystyle \cos \theta \geq 0}
cos
2
θ
=
cos
θ
{\displaystyle {\sqrt {\cos ^{2}\theta }}=\cos \theta }
Luego
∫
a
2
−
x
2
d
x
=
∫
a
2
−
a
2
sen
2
θ
(
a
cos
θ
)
d
θ
=
∫
a
2
(
1
−
sen
2
θ
)
(
a
cos
θ
)
d
θ
=
∫
a
2
(
cos
2
θ
)
(
a
cos
θ
)
d
θ
=
∫
(
a
cos
θ
)
(
a
cos
θ
)
d
θ
=
a
2
∫
cos
2
θ
d
θ
=
a
2
∫
(
1
+
cos
2
θ
2
)
d
θ
=
a
2
2
(
θ
+
1
2
sen
2
θ
)
+
C
=
a
2
2
(
θ
+
sen
θ
cos
θ
)
+
C
=
a
2
2
(
arcsen
(
x
a
)
+
x
a
1
−
x
2
a
2
)
+
C
=
a
2
2
arcsen
(
x
a
)
+
x
2
a
2
−
x
2
+
C
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\operatorname {sen} \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left({\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\;{\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C\end{aligned}}}
Para una integral definida, los límites de integración cambian una vez que se realiza la sustitución y estos están determinados por
θ
=
arcsen
(
x
a
)
{\displaystyle \theta ={\text{arcsen}}\left({\frac {x}{a}}\right)}
con valores para
θ
{\displaystyle \theta }
−
π
2
≤
θ
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}}
Considérese la integral definida
∫
−
1
1
4
−
x
2
d
x
{\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx}
que puede ser evaluada haciendo el cambio de variable
x
=
2
sen
θ
d
x
=
2
cos
θ
d
θ
{\displaystyle {\begin{aligned}x&=2\operatorname {sen} \theta \\dx&=2\cos \theta \,d\theta \end{aligned}}}
y en este caso, los límites de integración estarán determinados por
θ
=
arcsen
(
x
2
)
{\displaystyle \theta ={\text{arcsen}}\left({\frac {x}{2}}\right)}
Tenemos que
si
x
=
−
1
{\displaystyle x=-1}
θ
=
arcsen
(
−
1
2
)
=
−
π
6
{\displaystyle \theta ={\text{arcsen}}\left(-{\frac {1}{2}}\right)=-{\frac {\pi }{6}}}
y si
x
=
1
{\displaystyle x=1}
θ
=
arcsen
(
1
2
)
=
π
6
{\displaystyle \theta ={\text{arcsen}}\left({\frac {1}{2}}\right)={\frac {\pi }{6}}}
entonces
∫
−
1
1
4
−
x
2
d
x
=
∫
−
π
/
6
π
/
6
4
−
4
sen
2
θ
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
4
(
1
−
sen
2
θ
)
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
4
(
cos
2
θ
)
(
2
cos
θ
)
d
θ
=
∫
−
π
/
6
π
/
6
(
2
cos
θ
)
(
2
cos
θ
)
d
θ
=
4
∫
−
π
/
6
π
/
6
cos
2
θ
d
θ
=
4
∫
−
π
/
6
π
/
6
(
1
+
cos
2
θ
2
)
d
θ
=
2
[
θ
+
1
2
sen
2
θ
]
−
π
/
6
π
/
6
=
[
2
θ
+
sen
2
θ
]
|
−
π
/
6
π
/
6
=
(
π
3
+
sen
π
3
)
−
(
−
π
3
+
sen
(
−
π
3
)
)
=
2
π
3
+
3
{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\operatorname {sen} ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\operatorname {sen} ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right]_{-\pi /6}^{\pi /6}\\[6pt]&=[2\theta +\operatorname {sen} 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\operatorname {sen} {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\operatorname {sen} \left(-{\frac {\pi }{3}}\right)\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}
Por otro lado, si aplicamos directamente los límites de integración para la fórmula de la antiderivada obtenemos
∫
−
1
1
4
−
x
2
d
x
=
[
2
arcsen
(
x
2
)
+
x
2
4
−
x
2
]
−
1
1
=
(
2
arcsen
(
1
2
)
+
1
2
3
)
−
(
2
arcsen
(
−
1
2
)
−
1
2
3
)
=
(
2
⋅
π
6
+
3
2
)
−
(
2
⋅
(
−
π
6
)
−
3
2
)
=
2
π
3
+
3
{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[2\;{\text{arcsen}}\left({\frac {x}{2}}\right)+{\frac {x}{2}}{\sqrt {4-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\;{\text{arcsen}}\left({\frac {1}{2}}\right)+{\frac {1}{2}}{\sqrt {3}}\right)-\left(2\;{\text{arcsen}}\left(-{\frac {1}{2}}\right)-{\frac {1}{2}}{\sqrt {3}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}
a
2
+
x
2
{\displaystyle a^{2}+x^{2}}
[ editar ] Se hace el cambio de variable
x
=
a
tan
θ
{\displaystyle x=a\tan \theta }
identidad trigonométrica
sec
2
(
θ
)
−
tan
2
(
θ
)
=
1
{\displaystyle \sec ^{2}(\theta )-\tan ^{2}(\theta )=1}
Construcción geométrica para Caso
II
{\displaystyle {\text{II}}}
En la integral
∫
d
x
a
2
+
x
2
{\displaystyle \int {\frac {dx}{a^{2}+x^{2}}}}
hacemos el cambio de variable
x
=
a
tan
θ
d
x
=
a
sec
2
θ
d
θ
θ
=
arctan
(
x
a
)
{\displaystyle {\begin{aligned}x&=a\tan \theta \\dx&=a\sec ^{2}\theta \;d\theta \\\theta &=\arctan \left({\frac {x}{a}}\right)\end{aligned}}}
de modo que la integral se convierte en
∫
d
x
a
2
+
x
2
=
∫
a
sec
2
θ
a
2
+
a
2
tan
2
θ
d
θ
=
∫
a
sec
2
θ
a
2
(
1
+
tan
2
θ
)
d
θ
=
∫
a
sec
2
θ
a
2
sec
2
θ
d
θ
=
1
a
∫
d
θ
=
θ
a
+
C
=
1
a
arctan
(
x
a
)
+
C
{\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\,d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}(1+\tan ^{2}\theta )}}\;d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}\sec ^{2}\theta }}\,d\theta \\[6pt]&={\frac {1}{a}}\int d\theta \\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C\end{aligned}}}
para
a
≠
0
{\displaystyle a\neq 0}
La integral
∫
a
2
+
x
2
d
x
{\displaystyle \int {\sqrt {a^{2}+x^{2}}}\,{dx}}
puede ser evaluada haciendo el cambio de variable
x
=
a
tan
θ
d
x
=
a
sec
2
θ
d
θ
θ
=
arctan
(
x
a
)
{\displaystyle {\begin{aligned}x&=a\tan \theta \\dx&=a\sec ^{2}\theta \,d\theta \\\theta &=\arctan \left({\frac {x}{a}}\right)\end{aligned}}}
donde
a
>
0
{\displaystyle a>0}
a
2
=
a
{\displaystyle {\sqrt {a^{2}}}=a}
−
π
2
<
θ
<
π
2
{\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}}
por lo que
sec
θ
>
0
{\displaystyle \sec \theta >0}
sec
2
θ
=
sec
θ
{\displaystyle {\sqrt {\sec ^{2}\theta }}=\sec \theta }
Entonces
∫
a
2
+
x
2
d
x
=
∫
a
2
+
a
2
tan
2
θ
(
a
sec
2
θ
)
d
θ
=
∫
a
2
(
1
+
tan
2
θ
)
(
a
sec
2
θ
)
d
θ
=
∫
a
2
sec
2
θ
(
a
sec
2
θ
)
d
θ
=
∫
(
a
sec
θ
)
(
a
sec
2
θ
)
d
θ
=
a
2
∫
sec
3
θ
d
θ
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}}
La integral de la secante cúbica puede ser evaluada utilizando integración por partes , dando como resultado
∫
a
2
+
x
2
d
x
=
a
2
2
(
sec
θ
tan
θ
+
ln
|
sec
θ
+
tan
θ
|
)
+
C
=
a
2
2
(
1
+
x
2
a
2
⋅
x
a
+
ln
|
1
+
x
2
a
2
+
x
a
|
)
+
C
=
1
2
(
x
a
2
+
x
2
+
a
2
ln
|
x
+
a
2
+
x
2
|
)
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|x+{\sqrt {a^{2}+x^{2}}}\right|\right)+C.\end{aligned}}}
Para una integral definida, los límites de integración cambian una vez que se hace la sustitución y estos están determinados por
θ
=
arctan
(
x
a
)
{\displaystyle \theta =\arctan \left({\frac {x}{a}}\right)}
con valores para
θ
{\displaystyle \theta }
−
π
2
<
θ
<
π
2
{\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}}
Considérese la integral definida
∫
0
1
4
1
+
x
2
d
x
{\displaystyle \int _{0}^{1}{\frac {4}{1+x^{2}}}\,dx}
esta puede ser evaluada haciendo el cambio de variable
x
=
tan
θ
d
x
=
sec
2
θ
d
θ
{\displaystyle {\begin{aligned}x&=\tan \theta \\dx&=\sec ^{2}\theta \,d\theta \end{aligned}}}
con los límites de integración determinados por
θ
=
arctan
x
{\displaystyle \theta =\arctan x}
Tenemos que
si
x
=
0
{\displaystyle x=0}
θ
=
arctan
(
0
)
=
0
{\displaystyle \theta =\arctan(0)=0}
y si
x
=
1
{\displaystyle x=1}
θ
=
arctan
(
1
)
=
π
4
{\displaystyle \theta =\arctan(1)={\frac {\pi }{4}}}
de modo que
∫
0
1
4
1
+
x
2
d
x
=
4
∫
0
π
/
4
sec
2
θ
1
+
tan
2
θ
d
θ
=
4
∫
0
π
/
4
sec
2
θ
sec
2
θ
d
θ
=
4
∫
0
π
/
4
d
θ
=
4
θ
|
0
π
/
4
=
4
(
π
4
)
=
π
{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4}{1+x^{2}}}\;dx&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{1+\tan ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{\sec ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=4\theta {\Bigg |}_{0}^{\pi /4}\\&=4\left({\frac {\pi }{4}}\right)\\&=\pi \end{aligned}}}
x
2
−
a
2
{\displaystyle x^{2}-a^{2}}
[ editar ] Se hace el cambio de variable
x
=
a
sec
θ
{\displaystyle x=a\sec \theta }
identidad trigonométrica
sec
2
(
θ
)
−
tan
2
(
θ
)
=
1
{\displaystyle \sec ^{2}(\theta )-\tan ^{2}(\theta )=1}
Construcción geométrica para Caso
III
{\displaystyle {\text{III}}}
La integral
∫
d
x
x
2
−
a
2
{\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}}
también puede ser evaluada utilizando fracciones parciales en lugar de utilizar sustitución trigonométrica. Sin embargo, la integral
∫
x
2
−
a
2
d
x
{\displaystyle \int {\sqrt {x^{2}-a^{2}}}\,dx}
no. En este caso, una sustitución apropiada es
x
=
a
sec
θ
d
x
=
a
sec
θ
tan
θ
d
θ
θ
=
arcsec
(
x
a
)
{\displaystyle {\begin{aligned}x&=a\sec \theta \\dx&=a\sec \theta \tan \theta \,d\theta \\\theta &=\operatorname {arcsec} \left({\frac {x}{a}}\right)\end{aligned}}}
donde
a
>
0
{\displaystyle a>0}
a
2
=
a
{\displaystyle {\sqrt {a^{2}}}=a}
0
≤
θ
<
π
2
{\displaystyle 0\leq \theta <{\frac {\pi }{2}}}
suponiendo que
x
>
0
{\displaystyle x>0}
tan
θ
≥
0
{\displaystyle \tan \theta \geq 0}
tan
2
θ
=
tan
θ
{\displaystyle {\sqrt {\tan ^{2}\theta }}=\tan \theta }
Entonces,
∫
x
2
−
a
2
d
x
=
∫
a
2
sec
2
θ
−
a
2
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
(
sec
2
θ
−
1
)
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
tan
2
θ
⋅
a
sec
θ
tan
θ
d
θ
=
∫
a
2
sec
θ
tan
2
θ
d
θ
=
a
2
∫
(
sec
θ
)
(
sec
2
θ
−
1
)
d
θ
=
a
2
∫
(
sec
3
θ
−
sec
θ
)
d
θ
{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta \end{aligned}}}
Uno puede evaluar la integral de la función secante multiplicando tanto el numerador como el denominador por
(
sec
θ
+
tan
θ
)
{\displaystyle (\sec \theta +\tan \theta )}
[ 3]
∫
x
2
−
a
2
d
x
=
a
2
2
(
sec
θ
tan
θ
+
ln
|
sec
θ
+
tan
θ
|
)
−
a
2
ln
|
sec
θ
+
tan
θ
|
+
C
=
a
2
2
(
sec
θ
tan
θ
−
ln
|
sec
θ
+
tan
θ
|
)
+
C
=
a
2
2
(
x
a
⋅
x
2
a
2
−
1
−
ln
|
x
a
+
x
2
a
2
−
1
|
)
+
C
=
1
2
(
x
x
2
−
a
2
−
a
2
ln
|
x
+
x
2
−
a
2
a
|
)
+
C
.
{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}
[ editar ] La sustitución de una nueva variable por una función trigonométrica en ocasiones puede ser usada para facilitar el cálculo de la integral, dejando el integrando sin funciones trigonométricas.
∫
f
(
sen
(
x
)
,
cos
(
x
)
)
d
x
=
∫
1
±
1
−
u
2
f
(
u
,
±
1
−
u
2
)
d
u
u
=
sen
(
x
)
∫
f
(
sen
(
x
)
,
cos
(
x
)
)
d
x
=
∫
1
∓
1
−
u
2
f
(
±
1
−
u
2
,
u
)
d
u
u
=
cos
(
x
)
∫
f
(
sen
(
x
)
,
cos
(
x
)
)
d
x
=
∫
2
1
+
u
2
f
(
2
u
1
+
u
2
,
1
−
u
2
1
+
u
2
)
d
u
u
=
tan
(
x
2
)
{\displaystyle {\begin{aligned}\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}\;f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\operatorname {sen}(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}\;f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}\;f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\tfrac {x}{2}}\right)\\[6pt]\end{aligned}}}
La última sustitución es conocida como la Sustitución de Weierstrass , que hace uso de las fórmulas de la tangente del ángulo mitad .
Considérese la integral
∫
4
cos
x
(
1
+
cos
x
)
3
d
x
{\displaystyle \int {\frac {4\cos x}{(1+\cos x)^{3}}}\;dx}
Si utilizamos la sustitución de Weierstrass entonces
∫
4
cos
x
(
1
+
cos
x
)
3
d
x
=
∫
2
1
+
u
2
4
(
1
−
u
2
1
+
u
2
)
(
1
+
1
−
u
2
1
+
u
2
)
3
d
u
=
∫
(
1
−
u
2
)
(
1
+
u
2
)
d
u
=
∫
(
1
−
u
4
)
d
u
=
u
−
u
5
5
+
C
=
tan
(
x
2
)
−
1
5
tan
5
(
x
2
)
+
C
{\displaystyle {\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du\\&=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du\\&=u-{\frac {u^{5}}{5}}+C\\&=\tan \left({\frac {x}{2}}\right)-{\frac {1}{5}}\tan ^{5}\left({\frac {x}{2}}\right)+C\end{aligned}}}
[ editar ] También se pueden utilizar sustituciones mediante funciones hiperbólicas para simplificar determinadas integrales.[ 4]
Por ejemplo, en la integral
∫
1
a
2
+
x
2
d
x
{\displaystyle \int {\frac {1}{\sqrt {a^{2}+x^{2}}}}\,dx}
se realiza la sustitución
x
=
a
sinh
u
{\displaystyle x=a\sinh {u}}
d
x
=
a
cosh
u
d
u
.
{\displaystyle dx=a\cosh u\,du.}
Entonces, usando las identidades
cosh
2
(
x
)
−
sinh
2
(
x
)
=
1
{\displaystyle \cosh ^{2}(x)-\sinh ^{2}(x)=1}
sinh
−
1
x
=
ln
(
x
+
x
2
+
1
)
,
{\displaystyle \sinh ^{-1}{x}=\ln(x+{\sqrt {x^{2}+1}}),}
∫
1
a
2
+
x
2
d
x
=
∫
a
cosh
u
a
2
+
a
2
sinh
2
u
d
u
=
∫
a
cosh
u
a
1
+
sinh
2
u
d
u
=
∫
a
cosh
u
a
cosh
u
d
u
=
u
+
C
=
sinh
−
1
x
a
+
C
=
ln
(
x
2
a
2
+
1
+
x
a
)
+
C
=
ln
(
x
2
+
a
2
+
x
a
)
+
C
{\displaystyle {\begin{aligned}\int {\frac {1}{\sqrt {a^{2}+x^{2}}}}\,dx&=\int {\frac {a\cosh u}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a{\sqrt {1+\sinh ^{2}{u}}}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C\\[6pt]&=\ln \left({\sqrt {{\frac {x^{2}}{a^{2}}}+1}}+{\frac {x}{a}}\right)+C\\[6pt]&=\ln \left({\frac {{\sqrt {x^{2}+a^{2}}}+x}{a}}\right)+C\end{aligned}}}










![{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta }{\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\;d\theta \\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&={\text{arcsen}}\left({\frac {x}{a}}\right)+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c33cee5a81fe5b1fc55154b51e4ebb497aa176b)





















![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\operatorname {sen} \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left({\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\;{\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d4616bf2e80282227306399174c44ba7787196)








![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\operatorname {sen} ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\operatorname {sen} ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right]_{-\pi /6}^{\pi /6}\\[6pt]&=[2\theta +\operatorname {sen} 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\operatorname {sen} {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\operatorname {sen} \left(-{\frac {\pi }{3}}\right)\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb3b420d72073bb0cc67483388d2dd9e7d9b1c4)
![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[2\;{\text{arcsen}}\left({\frac {x}{2}}\right)+{\frac {x}{2}}{\sqrt {4-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\;{\text{arcsen}}\left({\frac {1}{2}}\right)+{\frac {1}{2}}{\sqrt {3}}\right)-\left(2\;{\text{arcsen}}\left(-{\frac {1}{2}}\right)-{\frac {1}{2}}{\sqrt {3}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a30c5d7cd0d8b39715021f705e76be11dcfa5e1)






![{\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\,d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}(1+\tan ^{2}\theta )}}\;d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}\sec ^{2}\theta }}\,d\theta \\[6pt]&={\frac {1}{a}}\int d\theta \\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5b087324f1c492895eac14832e631d2478e8fff)






![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/108a5f1becea83b5cb41021d81544ff3e1bab889)
![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|x+{\sqrt {a^{2}+x^{2}}}\right|\right)+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b72bbed5d6bbb2d3dff666fda9985029351c25a)







![{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4}{1+x^{2}}}\;dx&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{1+\tan ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{\sec ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=4\theta {\Bigg |}_{0}^{\pi /4}\\&=4\left({\frac {\pi }{4}}\right)\\&=\pi \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09938a7ac146b25472d7a851dd9a7d68b57de4df)












![{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d551bea9f1a33df981d45ab8cf11a1443d6da85)
![{\displaystyle {\begin{aligned}\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}\;f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\operatorname {sen}(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}\;f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}\;f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\tfrac {x}{2}}\right)\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4b07688dbf8f93a45c673360d666c378ecf2f09)







![{\displaystyle {\begin{aligned}\int {\frac {1}{\sqrt {a^{2}+x^{2}}}}\,dx&=\int {\frac {a\cosh u}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a{\sqrt {1+\sinh ^{2}{u}}}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C\\[6pt]&=\ln \left({\sqrt {{\frac {x^{2}}{a^{2}}}+1}}+{\frac {x}{a}}\right)+C\\[6pt]&=\ln \left({\frac {{\sqrt {x^{2}+a^{2}}}+x}{a}}\right)+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4de72234865476739112fe15f4849d934ebb1622)