1 + 2 + 3 + 4 + ⋯

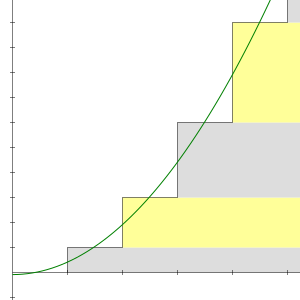
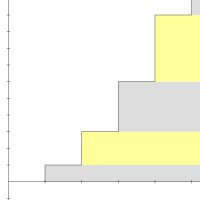
La suma infinita cuyos términos son los números naturales 1 + 2 + 3 + 4 + ⋯ es una serie divergente. La n-ésima suma parcial de la serie es el número triangular
que incrementa sin límite mientras n tiende al infinito. Ya que la sucesión de sumas parciales no converge a un límite finito, la serie no tiene una suma.
Aunque a primera vista parece que la serie no tiene ningún valor significativo, puede ser manipulada para producir varios resultados matemáticamente interesantes, algunos de los cuales tienen aplicaciones en otras áreas como el análisis complejo, la teoría cuántica de campos y la teoría de cuerdas. Varios métodos de suma se usan en matemáticas para asignarle valores numéricos a series divergentes. En particular, los métodos de regularización de la función zeta y el sumatorio de Ramanujan le asignan un valor de -112, que está expresado por una fórmula famosa:[2]
donde el lado izquierdo debe interpretarse como el valor obtenido utilizando uno de los métodos de suma antes mencionados y no como la suma de una serie infinita en su significado habitual. Estos métodos tienen aplicaciones en otros campos como el análisis complejo, la teoría cuántica de campos y la teoría de cuerdas.[3]
En una monografía sobre la teoría moonshine, el matemático Terry Gannon, de la Universidad de Alberta, califica esta ecuación de "una de las fórmulas más notables de la ciencia".[4]
Sumas parciales[editar]

Las sumas parciales de la serie 1 + 2 + 3 + 4 + 5 + ⋯ son 1, 3, 6, 10, 15, etc. La n-ésima suma parcial está dada por una fórmula simple:
Esta ecuación ya era conocida por los Pitagóricos desde al menos el siglo VI a. C..[5] Los números que cumplen esta forma se llaman números triangulares porque pueden ser acomodados para formar un triángulo equilátero.
La sucesión infinita de números triangulares diverge hacia +∞, así que por definición la serie infinita 1 + 2 + 3 + 4 + ⋯ también diverge a +∞. La divergencia es una simple consecuencia de la forma de la serie: los términos no se acercan a cero, así que la serie diverge por el test del término.
Sumabilidad[editar]
Entre las series clásicas divergentes, 1 + 2 + 3 + 4 + ⋯ es relativamente difícil de manipular hacia un valor finito. Muchos métodos de suma se usan para asignar valores numéricos a las series divergentes, algunos son más poderosos que otros. Por ejemplo, la sumación de Cesàro es un método reconocido que suma la serie de Grandi, la serie levemente divergente 1 − 1 + 1 − 1 + ⋯, a 12. La suma de Abel es un método más poderoso que no solo suma la serie de Grandia a 12, sino que también suma la serie más compleja 1 − 2 + 3 − 4 + ⋯ a 14.
A diferencia de las series anteriores, 1 + 2 + 3 + 4 + ⋯ no se puede sumar a través de la sumación de Cesàro ni la de Abel. Esos métodos funcionan en series divergentes que oscilan, pero no pueden producir una respuesta finita para series que divergen a +∞.[6] La mayoría de las definiciones más elementales de la suma de una serie divergente son estables y lineales, y cualquier método que es tanto estable y lineal no puede sumar 1 + 2 + 3 + ⋯ a un valor finito; véase más abajo. Se requieren métodos más avanzados, como la regularización de la función zeta o el sumatorio de Ramanujan. También es posible argumentar el valor de −112 usando heurísticas grosso modo relacionadas con estos métodos.
Heurística[editar]

Srinivasa Ramanujan presentó dos derivaciones de "1 + 2 + 3 + 4 + ⋯ = −112" en el capítulo 8 de su primer cuaderno.[7][8][9] la derivación más simple y menos rigurosa ocurre en dos pasos, de la siguiente forma.
La primera intuición clave es que la serie de números positivos 1 + 2 + 3 + 4 + ⋯ es parecida a la serie alternada 1 − 2 + 3 − 4 + ⋯. La última serie también es divergente, pero es más fácil trabajar con ella; hay varios métodos clásicos que le asignan un valor, que han sido explorados desde el siglo xviii.[10]
A fin de transformar la serie 1 + 2 + 3 + 4 + ⋯ en 1 − 2 + 3 − 4 + ⋯, es posible restarle 4 al segundo término, 8 al cuarto término, 12 al sexto término, y continuar. La cantidad total que debe ser restada es 4 + 8 + 12 + 16 + ⋯, que es 4 veces la serie original. Estas relaciones pueden ser expresadas con un poco de álgebra. Cualquiera que sea la "suma" de la serie, se puede llamar c = 1 + 2 + 3 + 4 + ⋯. Entonces, se multiplica esta ecuación por 4 y se resta la segunda ecuación de la primera:
La segunda intuición clave es que la serie alternada 1 − 2 + 3 − 4 + ⋯ es la expansión formal de la serie de potencias de la función 1(1 + x)2, donde x se define como 1. De acuerdo con esto, escribe Ramanujan:
Al dividir ambos lados por -3, se obtiene c = −112.
Hablando de forma general, es incorrecto manipular series infinitas como si fueran sumas finitas. Por ejemplo, si se insertaran ceros en posiciones arbitrarias de una serie divergente, es posible llegar a resultados que no son consistentes consigo mismos, menos aún con otros métodos. En particular, el paso 4c = 0 + 4 + 0 + 8 + ⋯ no está justificado por la ley de la identidad aditiva. Como ejemplo extremo, añadir un solo cero al inicio de la serie puede llevar a resultados inconsistentes.[1]
Una forma de remediar esta situación, y de limitar los sitios donde se pueden insertar los ceros, es llevar un registro de cada término en la serie al adjuntar una dependencia sobre alguna función.[Nota 1] En la serie 1 + 2 + 3 + 4 + ⋯, cada término n es solo un número. Si el término n es "promovido" a una función n−s, donde s es una variable compleja, entonces se puede asegurar que solo se añaden términos similares. La serie resultante puede ser manipulada con mayor rigor, y la variable s puede ser definida como −1 después. La implementación de esta estrategia se conoce como regularización de la función zeta.
Regularización de la función zeta[editar]

En la regularización de la función zeta, la serie es reemplazada por la serie . La segunda serie es ejemplo de una serie de Dirichlet. Cuando la parte real de s es mayor que 1, la serie Dirichlet converge, y su suma es la función zeta de Riemann ζ(s). Por otra parte, la serie de Dirichlet diverge cuando la parte real de s es menor que o igual a 1, así que, en particular, la serie 1 + 2 + 3 + 4 + ⋯ que resulta de declarar s = –1 no converge. El beneficio de introducir la función zeta de Riemann es que puede ser definida para otros valores de s por continuación analítica. Entonces es posible definir la suma zeta regularizada de 1 + 2 + 3 + 4 + ⋯ para ser ζ(−1).
Desde este punto, hay varias formas de probar que ζ(−1) = −112. Un método, sobre las líneas de razonamiento de Euler,[12] usa la relación entre la función zeta de Riemann y la función eta de Dirichlet η(s). La función zeta está definida por una serie alternada de Dirichlet, así que este método es paralelo a la heurística previa. Donde ambas series de Dirichlet converge, una tiene las identidades:
La identidad sigue siendo verdadera cuando ambas funciones se extienden por continuación analítica para incluir valores de s para los cuales la serie arriba mencionada diverge. Sustituyendo s = −1, se obtiene −3ζ(−1) = η(−1). Ahora, calculando η(−1) es una tarea más sencilla, ya que la función eta es igual a la suma de Abel de las serie que la define,[11]: 490–492 que es un límite de un lado:
Al dividir ambos lados por −3, se obtiene ζ(−1) = −112.
Regularización de corte[editar]
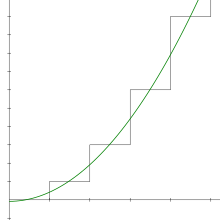
El método de regularización usando una función de corte puede "suavizar" la serie para llegar a −112. El "suavizado" es un puente conceptual entre la regularización de la función zeta, con su dependencia en el análisis complejo, y el sumatorio de Ramanujan, con su atajo a la fórmula de Euler-Maclaurin. En lugar de ello, el método opera directamente en transformaciones conservativas de la serie, usando métodos del análisis real.
La idea es reemplazar la serie discreta de mal comportamiento con una versión suavizada
- ,
donde f es una función de corte con propiedades apropiadas. La función de corte debe ser normalizada a f(0) = 1; esto es una normalización diferente a la usada en ecuaciones diferenciales. La función de corte debe tener suficientes derivadas acotadas para suavizar los picos o "arrugas" de la serie, y debería decaer a 0 más rápido que lo que crece la serie. Por conveniencia, se puede requerir que f sea una función continuamente diferenciable, acotada y con soporte compacto. Entonces se puede probar que esta suma continua es asintótica a −112 + CN2, donde C es una constante que depende de f. El término constante de la expansión asintótica no depende de f: es necesariamente el mismo valor dado por la continuación analítica, −112.[1]
Sumatorio de Ramanujan[editar]
La suma de Ramanujan de 1 + 2 + 3 + 4 + ⋯ también es −112. Ramanujan escribió en su segunda carta a G. H. Hardy, con fecha del 27 de febrero de 1913:[13]
Dear Sir, I am very much gratified on perusing your letter of the 8th February 1913. I was expecting a reply from you similar to the one which a Mathematics Professor at London wrote asking me to study carefully Bromwich's Infinite Series and not fall into the pitfalls of divergent series. … I told him that the sum of an infinite number of terms of the series: 1 + 2 + 3 + 4 + ⋯ = −112 under my theory. If I tell you this you will at once point out to me the lunatic asylum as my goal. I dilate on this simply to convince you that you will not be able to follow my methods of proof if I indicate the lines on which I proceed in a single letter. …Estimado Señor, estoy muy satisfecho de examinar su carta del 8 de febrero de 1913. Esperaba una respuesta de usted similar a la que un profesor de matemáticas en Londres me escribió pidiéndome estudiar cuidadosamente Series infinitas de Bromwich y no caer en la trampa de series divergentes. … Le dije que la suma de un número infinito de términos de la serie 1 + 2 + 3 + 4 + ⋯ = −112 de acuerdo con mi teoría. Si le digo esto, usted inmediatamente me indicará el camino al asilo de lunáticos como mi meta. He demorado en esto simplemente para convencerle que no será capaz de seguir mis métodos de prueba si yo indico las líneas sobre las cuales puedo proceder en una sola carta. …
El sumatorio de Ramanujan es un método para aislar el término constante en la fórmula de Euler-Maclaurin para la suma parcial de una serie. Para una función f, la suma clásica de Ramanujan para la serie se define de la siguiente forma:
donde f(2k−1) es la (2k − 1)-ésima derivada de f y B2k es el 2k-ésimo número de Bernoulli: B2 = 16, B4 = −130, y así sucesivamente. Estableciendo f(x) = x, la primera derivada de f es 1, y todos los demás términos desaparecen, y entonces:[14]
Para evitar inconsistencias, la teoría moderna de sumas de Ramanujan requiere que f sea "regular" en el sentido que las derivadas de órdenes mayores de f decaigan lo suficientemente rápido para que el resto de los términos en la fórmula Euler-Maclaurin tiendan a 0. Ramanujan tácitamente asumió esta propiedad.[14] El requisito de regularidad previene el uso de un sumatorio de Ramanujan sobre series espaciadas como 0 + 2 + 0 + 4 + ⋯, porque no hay función regular que tome esos valores. En lugar de ello, una serie así debe ser interpretada por la regularización de la función zeta. Por esta razón, Hardy recomienda "gran precaución" al aplicar las sumas de Ramanujan de series conocidas para encontrar las sumas de series relacionadas.[15]
Fracaso de los métodos estables de sumación lineal[editar]
Un método de sumación que es estable y lineal no puede sumar la serie 1 + 2 + 3 + ⋯ a ningún valor finito.[16] (Estable quiere decir que añadir un término al inicio de la serie incrementa la suma por esa misma cantidad.) Esto se puede ver de la siguiente forma. Si
- 1 + 2 + 3 + ⋯ = x
entonces añadiendo 0 a ambos lados da
- 0 + 1 + 2 + ⋯ = 0 + x = x por estabilidad.
Por linearidad, uno puede sustraer la segunda ecuación de la primera para dar
- 1 + 1 + 1 + ⋯ = x – x = 0.
Añadiendo 0 a ambos lados de nuevo da
- 0 + 1 + 1 + 1 + ⋯ = 0,
y sustrayendo las últimas dos series da
- 1 + 0 + 0 + ⋯ = 0
lo cual contradice la estabilidad.
Los métodos arriba mencionados para sumar 1 + 2 + 3 + ⋯ No son ni estables ni lineales.[17]
Física[editar]
En la teoría de cuerdas bosónica, el intento es computar los posibles niveles de energía de una cuerda, en particular la del nivel de energía más bajo. De manera informal, cada armónico de la cuerda se puede ver como una colección de D − 2 osciladores armónicos cuánticos, uno por cada dirección transversal, donde D es la dimensión del espacio-tiempo. Si la frecuencia fundamental de oscilación es ω entonces la energía en un oscilador que contribuye al n-ésimo armónico es nħω2. Así que usando la serie divergente, la suma sobre todos los armónicos es −ħω(D − 2)24. Últimamente es este hecho, combinado con el teorema de Goddard-Thorn, que lleva a la teoría de cuerdas bosónica a fracasar en ser consistente con dimensiones que no sean 26.[18]
La regularización de 1 + 2 + 3 + 4 + ⋯ también está involucrada en el cálculo de la fuerza de Casimir para un campo escalar en una dimensión.[Nota 2] Una función exponencial de corte es suficiente para normalizar la serie, representando el hecho de que los modos de energía arbitrariamente alta no están bloqueados por las placas de conducción. La simetría espacial del problema es responsable de cancelar el término cuadrático de la expansión. Todo lo que queda es el término constante −112, y el signo negativo de este resultado refleja el hecho de que la fuerza de Casimir es atractiva.[19]
Un cálculo similar está involucrado en tres dimensiones, usando la función zeta de Epstein en lugar de la función zeta de Riemann.[20]
Historia[editar]
No es claro si Leonhard Euler sumó la serie de −112. De acuerdo a Morris Kline, el trabajo temprano de Euler acerca de series divergentes se basaba en expansiones de funciones, de las cuales concluyó que 1 + 2 + 3 + 4 + ⋯ = ∞.[21] De acuerdo a Raymond Ayoub, el hecho de que la serie divergente zeta no es sumable por el método de Abel evitó que Euler usara la función zeta tan libremente como la función eta, y "no pudo asignarle un significado" a la serie.[22] Otros autores le dan a Euler el crédito de esta suma, sugiriendo que Euler habría extendido la relación entre las funciones zeta y eta a los números enteros negativos.[23][24][25] En la literatura primaria, la serie 1 + 2 + 3 + 4 + ⋯ es mencionada en la publicación de Euler de De seriebus divergentibus junto a la serie geométrica divergente 1 + 2 + 4 + 8 + ⋯. Euler sugiere que las series de este tipo tienen sumas finitas y negativas, y explica lo que esto quiere decir para las series geométricas, pero no regresa a discutir 1 + 2 + 3 + 4 + ⋯. En la misma publicación, Euler escribe que la suma de 1 + 1 + 1 + 1 + ⋯ es infinita.[26]
Otros medios[editar]
La novela de David Leavitt publicada en 2007, The Indian Clerk incluye una escena en la que Hardy y Littlewood discuten el significado de esta serie. Su conclusión es que Ramanujan ha redescubiertoζ(−1), y asumen que la frase acerca de un "asilo" en su segunda carta es una señal de que Ramanujan está solamente jugando con ellos.[27]
La obra de 2007 de Simon McBurney, A Disappearing Number se enfoca en esta serie en la primera escena. La protagonista, Ruth, entra a un salón e introduce la idea de una serie divergente antes de proclamar "Voy a mostrarles algo realmente emocionante," que es 1 + 2 + 3 + 4 + ⋯ = −112. Mientras Ruth se adentra en una derivación de la ecuación funcional de la función zeta, otro actor se dirige al público, admitiendo que son actores: "Pero las matemáticas son reales. Es terrorífico, pero es real."[28][29]
En enero de 2014, Numberphile produjo un video de YouTube acerca de esta serie, la cual fue vista más de 1.5 millones de veces en su primer mes.[30] El video de 8 minutos está narrado por Tony Padilla, un físico en la Universidad de Nottingham. Padilla comienza con 1 − 1 + 1 − 1 + ⋯ y 1 − 2 + 3 − 4 + ⋯ y relaciona esta última con 1 + 2 + 3 + 4 + ⋯ usando una resta término-por-término similar al argumento de Ramanujan.[31] Numberphile también lanzó una versión de 21 minutos del video, con el físico de la Universidad de Nottingham Ed Copeland, quien describe con mayor detalle cómo 1 − 2 + 3 − 4 + ⋯ = 14 como una suma de Abel y 1 + 2 + 3 + 4 + ⋯ = −112 como ζ(−1).[32] Después de que recibieron quejas sobre la falta de rigor en el primer video, Padilla también escribió una explicación en su página web en la que relaciona las manipulaciones en el video a identidades entre las continuaciones analíticas de las series de Dirichlet relevantes.[33]
En la cobertura del New York Times acerca del video de Numberphile, el matemático Edward Frenkel comentó que "este cálculo es uno de los secretos mejor guardados de las matemáticas. Nadie fuera de ellas lo conoce."[30]
La cobertura de este tema en la revista Smithsonian describe el video de Numberphile como engañoso, y anota que la interpretación de la suma como −112 se basa en un significado especializado para el signo igual que, por las técnicas de continuación analítica, en la que igual que quiere decir está asociado con.[34]
| Suma término por término usada en el video de Numberphile | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | = | 1 | + 2 | + 3 | + 4 | + 5 | + 6 | + 7 | + 8 | + … | = ? | |
| S1 | = | 1 | − 1 | + 1 | − 1 | + 1 | − 1 | + 1 | − 1 | + … | = 12 | |
| S2 | = | 1 | − 2 | + 3 | − 4 | + 5 | − 6 | + 7 | − 8 | + … | ||
| 2S2 | = | 1 | − 2 | + 3 | − 4 | + 5 | − 6 | + 7 | − 8 | + … | ||
| + 1 | − 2 | + 3 | − 4 | + 5 | − 6 | + 7 | + … | |||||
| = | 1 | − 1 | + 1 | − 1 | + 1 | − 1 | + 1 | − 1 | + … | = 12 | ||
| S2 | = 14 | |||||||||||
| S − | S2 | = | 1 | + 2 | + 3 | + 4 | + 5 | + 6 | + 7 | + 8 | + … | |
| − | 1 | + 2 | − 3 | + 4 | − 5 | + 6 | − 7 | + 8 | + … | |||
| = | 0 | + 4 | + 0 | + 8 | + 0 | + 12 | + 0 | + 16 | + … | = 4S | ||
| S – 14 = 4S ⇒ S = – 112 | ||||||||||||
Notas[editar]
- ↑ Se ha identificado la acción de promover números a funciones como una de las dos clases generales, incluyendo los sumatorios de Abel y Borel, de acuerdo a Knopp.[11]: 475–476
- ↑ Véase "Casimir effect in one dimension" en Wikiversidad en inglés
Referencias[editar]
- ↑ a b c d Tao, Terence (10 de abril de 2010), The Euler–Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation [La fórmula Euler-Maclaurin, números de Bernoulli, la función zeta y continuación analítica de variables reales], consultado el 30 de enero de 2014.
- ↑ Lepowsky, J. (1999), «Vertex operator algebras and the zeta function», en Naihuan Jing y Kailash C. Misra, ed., Recent Developments in Quantum Affine Algebras and Related Topics, Contemporary Mathematics 248, pp. 327-340, arXiv:math/9909178.
- ↑ Tong, David (February 23, 2012). "String Theory". pp. 28–48. arXiv:0908.0333 [hep-th].
- ↑ Gannon, Terry (April 2010), Moonshine Beyond the Monster: The Bridge Connecting Algebra, Modular Forms and Physics, Cambridge University Press, p. 140, ISBN 978-0521141888.
- ↑ Pengelley, David J. (2002), «The bridge between the continuous and the discrete via original sources», en Otto Bekken, ed., Study the Masters: The Abel-Fauvel Conference, National Center for Mathematics Education, University of Gothenburg, Sweden, p. 3, ISBN 978-9185143009.
- ↑ Hardy p.10
- ↑ Ramanujan's Notebooks, consultado el 26 de enero de 2014.
- ↑ Abdi, Wazir Hasan (1992), Toils and triumphs of Srinivasa Ramanujan, the man and the mathematician [Los esfuerzos y triunfos de Srinivasa Ramanujan, el hombre y el matemático], National, p. 41.
- ↑ Berndt, Bruce C. (1985), Ramanujan’s Notebooks: Part 1 [Los cuadernos de Ramanujan: parte 1], Springer-Verlag, pp. 135-136.
- ↑ Euler, Leonhard; Willis, Lucas (traductor); Osler, Thomas J. (traductor) (2006). «Translation with notes of Euler's paper: Remarks on a beautiful relation between direct as well as reciprocal power series» [Traducción con notas del artículo de Euler: Anotaciones sobre una hermosa relación entre tanto las series directas como las recíprocas]. The Euler Archive. Consultado el 22 de marzo de 2007. publicado originalmente como Euler, Leonhard (1768). «Remarques sur un beau rapport entre les séries des puissances tant directes que réciproques». Memoires de l'academie des sciences de Berlin 17: 83-106.
- ↑ a b Knopp, Konrad (1990) [1922]. Theory and Application of Infinite Series [Teoría y aplicación de series infinitas]. Dover. ISBN 0-486-66165-2.
- ↑ Stopple, Jeffrey (2003), A Primer of Analytic Number Theory: From Pythagoras to Riemann, p. 202, ISBN 0-521-81309-3.
- ↑ Ramanujan, Srinivasa Aiyangar (1995). Berndt, Bruce C.; Rankin, Robert Alexander, eds. Ramanujan: Letters and Commentary [Ramanujan: cartas y comentario]. History of Mathematics (en inglés estadounidense). American Mathematical Soc. p. 53. ISBN 9780821891254. Consultado el 30 de noviembre de 2016.
- ↑ a b Berndt, Bruce C. (1985), Ramanujan’s Notebooks: Part 1, Springer-Verlag, pp. 13, 134.
- ↑ Hardy p.346
- ↑ Shawyer, Bruce; Watson, Bruce (1994). Borel's methods of summability: theory and applications. Oxford mathematical monographs. Clarendon Press. ISBN 978-0-19-853585-0.
- ↑ «TEORÍA DE LOS ALGORITMOS LINEALES Y DE CONVERGENCIA Y DE SUMACIÓN». Librería Instituto de Estudios Riojanos. Consultado el 4 de julio de 2023.
- ↑ Barbiellini-Amidei, Bernardo (21 de mayo de 1987). «The Casimir effect in conformal field theories». Physics Letters B 190 (1): 137-139. doi:10.1016/0370-2693(87)90854-9. Consultado el 9 de diciembre de 2016.
- ↑ Zee, A (2003). Quantum field theory in a nutshell. Princeton, N.J: Princeton University Press. p. 65-67. ISBN 0-691-01019-6.
- ↑ Zeidler, Eberhard (2006). Quantum Field Theory I: Basics in Mathematics and Physics: A Bridge between Mathematicians and Physicists. Berlín: Springer. p. 305-306. ISBN 978-3-540-34764-4.
- ↑ Kline, Morris (16 de noviembre de 1983), «Euler and Infinite Series», Mathematics Magazine 56 (5): 307-314, doi:10.2307/2690371.
- ↑ Ayoub, Raymond (Diciembre de 1974), «Euler and the Zeta Function», The American Mathematical Monthly 81 (10): 1067-1086, doi:10.2307/2319041, consultado el 14 de febrero de 2014.
- ↑ Lefort, Jean, «Les séries divergentes chez Euler», l'Ouvert (IREM de Strasbourg) (31): 15-25, archivado desde el original el 22 de febrero de 2014, consultado el 14 de febrero de 2014.
- ↑ Kaneko, Masanobu; Kurokawa, Nobushige; Wakayama, Masato (2003). «A variation of Euler's approach to values of the Riemann zeta function». Kyushu Journal of Mathematics 57 (1): 175-192. arXiv:math/0206171. doi:10.2206/kyushujm.57.175. Archivado desde el original el 2 de febrero de 2014. Consultado el 31 de enero de 2014.
- ↑ Sondow, Jonathan (Febrero de 1994). «Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series». Proceedings of the American Mathematical Society 120 (4): 421-424. doi:10.1090/S0002-9939-1994-1172954-7. Consultado el 14 de febrero de 2014.
- ↑ Barbeau, E.J.; Leah, P.J. (Mayo de 1976), «Euler's 1760 paper on divergent series», Historia Mathematica 3 (2): 141-160, doi:10.1016/0315-0860(76)90030-6.
- ↑ Leavitt, David (2007). The Indian Clerk. Bloomsbury. pp. 61-62.
- ↑ Complicite (Abril de 2012), A Disappearing Number, Oberon.
- ↑ Thomas, Rachel (1 de diciembre de 2008), «A disappearing number», Plus, consultado el 5 de febrero de 2014.
- ↑ a b Overbye, Dennis (3 de febrero de 2014). «In the End, It All Adds Up to –1/12». New York Times. Consultado el 3 de febrero de 2014.
- ↑ ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = –1/12 en YouTube.
- ↑ Sum of Natural Numbers (second proof and extra footage) en YouTube.
- ↑ Padilla, Tony, What do we get if we sum all the natural numbers?, consultado el 3 de febrero de 2014.
- ↑ Schultz, Colin (31 de enero de 2014). «The Great Debate Over Whether 1+2+3+4..+ ∞ = −1/12». Smithsonian. Consultado el 16 de mayo de 2016.
Bibliografía[editar]
- Berndt, Bruce C.; Srinivasa Ramanujan Aiyangar (1995). Ramanujan: letters and commentary. American Mathematical Society. ISBN 0-8218-0287-9.
- Hardy, G. H. (1949). Divergent Series. Clarendon Press.
- Zee, A. (2003). Quantum field theory in a nutshell. Princeton UP. ISBN 0-691-01019-6.
Lecturas adicionales[editar]
- Lepowsky, James (1999). «Vertex operator algebras and the zeta function». Contemporary Mathematics 248: 327-340. arXiv:math/9909178. doi:10.1090/conm/248/03829.
- Zwiebach, Barton (2004). A First Course in String Theory. Cambridge UP. ISBN 0-521-83143-1. See p. 293.
- Elizalde, Emilio (2004). «Cosmology: Techniques and Applications». Proceedings of the II International Conference on Fundamental Interactions. arXiv:gr-qc/0409076.
- Watson, G. N. (16 de abril de 1929), «Theorems stated by Ramanujan (VIII): Theorems on Divergent Series», Journal of the London Mathematical Society, 1 4 (2): 82-86, doi:10.1112/jlms/s1-4.14.82.
Enlaces externos[editar]
- Series divergentes en Wikiversidad (en inglés)
- Lamb E. (2014), "Does 1+2+3… Really Equal –1/12?", Scientific American Blogs. (en inglés)
- This Week's Finds in Mathematical Physics (Week 124), (Week 126), (Week 147), (Week 213) (en inglés)
- Euler’s Proof That 1 + 2 + 3 + ⋯ = −1/12 – by John Baez (en inglés)
- García Moreta, José Javier http://prespacetime.com/index.php/pst/article/view/498 The Application of Zeta Regularization Method to the Calculation of Certain Divergent Series and Integrals Refined Higgs, CMB from Planck, Departures in Logic, and GR Issues & Solutions vol 4 N.º 3 prespacetime journal http://prespacetime.com/index.php/pst/issue/view/41/showToc (en inglés)
- John Baez (19 de septiembre de 2008). «My Favorite Numbers: 24». (en inglés)
- The Euler-Maclaurin formula, Bernoulli numbers, the zeta function, and real-variable analytic continuation por Terence Tao (en inglés)
- A recursive evaluation of zeta of negative integers by Luboš Motl (en inglés)
- Enlace al video de Numberphile: 1 + 2 + 3 + 4 + 5 + ... = –1/12Numberphile (en inglés)
- Sum of Natural Numbers (second proof and extra footage) incluye una demostración del método de Euler. (en inglés)
- What do we get if we sum all the natural numbers? response to comments about video by Tony Padilla (en inglés)
- Artículo relacionado del New York Times (en inglés)
- Why –1/12 is a gold nugget Video de seguimiento con Edward Frenkel (en inglés)
- Divergent Series: why 1 + 2 + 3 + ⋯ = −1/12 por Brydon Cais de la Universidad de Arizona (en inglés)