Conjunto de Delaunay

Los puntos rojos forman parte de una ε-red en el plano Euclidiano, donde ε es el radio de los discos amarillos grandes. Los discos azules (con la mitad de la radio que los amarillos) son disjuntos, y el conjunto de todos los discos amarillos cubre todo el plano, satisfaciendo los dos requisitos de la definición de una ε-red.

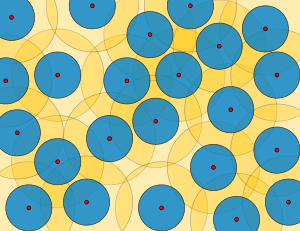
En la teoría matemática de espacios métricos, ε-redes, ε-empaquetados, ε-coberturas, conjuntos uniformemente discretos, conjuntos relativamente densos, y conjuntos de Delaunay (nombrados así en memoria del matemático ruso Borís Delaunay; también son denominados conjuntos de Delone) son muchas veces definiciones estrechamente relacionadas de conjuntos de puntos bien-ordenados, y la relación entre el radio de empaquetado y el radio de recubrimiento mide en qué grado están bien-ordenados. Estos conjuntos tienen aplicaciones en teoría de códigos, en algoritmos de aproximación, y en la teoría de cuasicristales.

Definiciones

Si (M,d) es un espacio métrico, y X es un subconjunto de M, entonces el radio de empaquetado de X es la mitad de la mínima de las distancias entre miembros distintos de X. Si el radio de empaquetamiento es r, entonces todas las bolas abiertas de radio r centradas en los puntos de X serán disjuntas entre sí, y cada bola abierta centrada en uno de los puntos de X con radio 2r será disjunta con respecto al resto de puntos de X. El radio de recubrimiento de X es el mínimo de los números r tal que cada punto de M está dentro de la distancia r de al menos un punto en X; esto es, es el radio más pequeño tal que la unión de las bolas cerradas de este radio centrado en los puntos de X contiene todo M. Un ε-empaquetado es un conjunto X de radios de empaquetado ≥ ε/2 (o lo que es lo mismo, con distancia mínima ≥ ε), un ε-recubrimiento es un conjunto X de radio de recubrimiento ≤ ε, y una ε-red es un conjunto que es a la vez un ε-empaquetado y un ε-recubrimiento. Un conjunto es uniformemente discreto si tiene un empaquetado de radio no nulo, y relativamente denso si tiene un radio de cobertura finito. Un conjunto de Delaunay es a la vez uniformemente discreto y relativamente denso; así, toda ε-red es un conjunto de Delaunay, pero no al revés.​​

Construcción de ε-redes

Siendo la más restrictiva de las definiciones anteriores, ε-redes son al menos tan difíciles de construir como los ε-empaquetados, los ε-recubrimientos, y los conjuntos de Delaunay. Aun así, siempre que los puntos de M son un conjunto bien ordenado, por un proceso de inducción transfinita es posible construir una ε-red N, incluyendo en N cada punto para el que la mínima de las distancias al conjunto de los anteriores puntos en la ordenación es al menos ε. Para conjuntos finitos de puntos en un espacio euclidiano de dimensión acotada, cada punto puede ser analizado en un tiempo finito localizándolo en una retícula de células de diámetro ε, utilizando un tabla hash para comprobar qué células cercanas ya contienen puntos de N; así, en este caso, una ε-red puede ser construida en un tiempo lineal.​​

Para espacios métricos finitos o compactos más generales, un algoritmo alternativo es el de Teo González, basado en el criterio del primer recorrido más lejano, que suele usarse para construir ε-redes finitas. Este algoritmo inicializa la red N vacía, añadiendo iterativamente a N el punto más lejano de M a N, rompiendo enlaces arbitrariamente y deteniéndose cuando todos los puntos de M quedan dentro de la distancia ε de N.​ En espacios de dimensión duplicada delimitada, el algoritmo de González puede ser implementado en un tiempo de O(n log n) para conjuntos de puntos con una proporción polinómica entre sus distancias más lejanas y más cercanas, y aproximadamente en el mismo límite de tiempo para conjuntos de puntos arbitrarios.​

Aplicaciones

Teoría de codificación

En la teoría de códigos de corrección de errores, el espacio métrico contiene un código de bloque C que consta de cadenas de una longitud fija, por ejemplo n, formadas sobre un alfabeto de q elementos (pueden ser visualizados como vectores), con la métrica de Hamming. Este espacio se denota como $\scriptstyle {\mathcal {A}}_{q}^{n}$. El radio de recubrimiento y de empaquetado de este espacio métrico está relacionado con la capacidad de corregir errores del código.

Algoritmos de aproximación

Har-Peled y Raichel (2013) & Raichel (2013) describieron un paradigma algorítmico que denominaron "red y ciruela pasa" para diseñar algoritmos de aproximación para ciertos tipos de problemas de optimización geométrica definidos en conjuntos de puntos en espacios euclidianos. Un algoritmo de este tipo trabaja siguiendo los pasos siguientes:

1. Escoger un punto aleatorio p del conjunto de puntos, encontrar su vecino más cercano q, y poner ε a la distancia entre p y q.
2. Probar si ε es (aproximadamente) mayor o menor que el valor de la solución óptima (utilizando una técnica específica para la optimización particular del problema que está siendo solucionado)
   • Si es mayor, eliminar de la entrada los puntos cuyo vecino más cercano es más lejano que ε
   • Si es más pequeño, construir una ε-red N, y eliminar de la entrada los puntos que no están en N.

En ambos casos, el número esperado de puntos restantes decrece por un factor constante, así que el tiempo de cálculo pasa a estar dominado por intervalo invertido en el paso de la prueba. Como demuestran, este paradigma se suele poder utilizar para construir algoritmos de aproximación rápida para nubes de k-centros, encontrando un par de puntos con distancia media, y resolver muchos otros problemas relacionados.

Un sistema jerárquico de redes, denominado una red-árbol, puede ser utilizado en espacios de dimensión duplicada delimitada para construir descomposiciones bien separadas, geometrías llave (geometric spanners), y en la búsqueda aproximada de puntos vecinos más cercanos.​​

Cristalografía

Para puntos en un espacio euclídeo, un conjunto X es un conjunto de Meyer si es relativamente denso y su conjunto de diferencias X − X es uniformemente discreto. De forma equivalente, X es un conjunto de Meyer si ambos X y X − X son conjuntos de Delaunay. Los conjuntos de Meyer deben su denominación a Yves Meyer, quien los introdujo (con una definición diferente pero equivalente basada en el análisis armónico) como modelo matemático para cuasicristales. Incluyen los conjuntos de puntos en retículas, teselaciones de Penrose, y las sumas de Minkowski de estos conjuntos con conjuntos finitos.​

Enlaces externos

• Delone set – Tilings Encyclopedia

• Datos: Q5254313