Distribución normal sesgada
| Distribución normal sesgada | ||
|---|---|---|
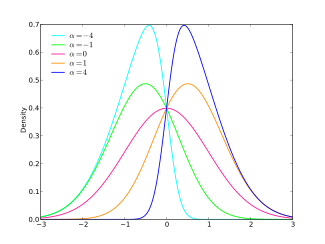 Función de densidad de probabilidad | ||
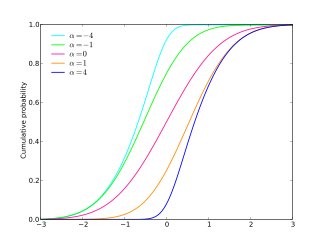 Función de distribución de probabilidad | ||
| Parámetros |
ubicación (real) escala (real positivo) forma (real) | |
| Dominio | ||
| Función de densidad (pdf) | ||
| Función de distribución (cdf) | ||
| Media | donde | |
| Moda | ||
| Curtosis | ||
| Función generadora de momentos (mgf) | ||
| Función característica | ||
En estadística y probabilidad, la distribución normal sesgada es una distribución de probabilidad continua que generaliza a la distribución normal permitiendo que el sesgo estadístico sea distinto de cero.
Definición[editar]
Sea la función de densidad de probabilidad para una distribución normal
con la función de distribución acumulada dada por
- ,
donde "erf" es la función error. Entonces, la función de densidad de probabilidad (comúnmente "PDF" por sus siglas en inglés) de la distribución normal sesgada con parámetro está dada por
La distribución fue descrita por primera vez por O'Hagan y Leonard en 1976.[1] Existen aproximaciones a la distribución que son matemáticamente más fáciles de manipular, presentadas por Ashour y Abdel-Hamid[2] y otra por Mudholkar y Hutson.[3]
Andel, Netuka y Zvara describieron un proceso estocástico subyacente a la distribución en 1984.[4] Tanto la distribución el proceso estocástico son consecuencias del argumento de simetría desarrollado por Chan y Tong (1986),[5] que se aplica a los casos multivariados más allá de la normalidad, como por ejemplo distribuciones t multivariadas. La distorsión es un caso particular de una clase general de distribuciones con funciones de densidad de probabilidad de la forma f(x)=2 φ(x) Φ(x) donde φ() es cualquier PDF simétrica alrededor del cero y Φ() es cualquier CDF cuya PDF es simétrica alrededor del cero.[6]
Para añadir parámetros de ubicación y escala a esta distribución, es usual hacer la transformación . Se puede verificar que la distribución normal se recupera cuando , y que el valor absoluto del sesgo incrementa a medida que el valor absoluto de incrementa. La distribución está sesgada hacia la derecha si y sesgada hacia la izquierda si . La función de la densidad de probabilidad con ubicación , escala , y parámetro se vuelve
Debe notarse, sin embargo, que el sesgo () de la distribución está limitado al intervalo .
Se ha demostrado,[7] que la moda (máximo) de la distribución es único. Para un en general, no existen expresiones analíticas para , aunque es posible conseguir una buena aproximación numérica con:
donde y
Estimación[editar]
Las estimaciones de máxima verosimilitud para , , y pueden ser calculados numéricamente, pero no existen expresiones en forma cerrada para estos estimados a menos que . Si es necesaria una expresión en forma cerrada, puede aplicarse el método de momentos para estimar a partir del sesgo muestra, mediante la inversión de la ecuación de sesgo. Esto da como resultado la estimación
donde , y es el sesgo muestra. El signo de debe ser el mismo signo que . En consecuencia, .
El sesgo máximo (teóricamente) se obtiene al establecer en la ecuación de sesgo, resultando en . Sin embargo, es posible que el sesgo muestra sea más grande, con lo que no podría ser determinado a partir de estas ecuaciones. Al usar el método de momentos de forma automática, por ejemplo para dar valores iniciales para la iteración de máxima verosimilitud, uno debería establecer (por ejemplo) que .
Existen, sin embargo, objeciones acerca del impacto de los métodos de sesgo normal y de qué tan confiables son las inferencias basadas en ellos.[8]
Distribuciones relacionadas[editar]
La distribución noremal modificada exponencialmente es otra distribución de 3 parámetros que generaliza a la distribución normal para incluir casos sesgados. La distribución normal sesgada mantiene una "cola" normal en la dirección del sesgo, con una "cola" más corta en la dirección opuesta; esto es, su densidad es asintóticamente proporcional a para un positivo. Por lo tanto en términos de los siete estados de aleatoriedad, presenta "aleatoriedad moderada propiamente". En contraste, la distribución normal modificada exponencialmente tiene una "cola" exponencial en la dirección del sesgo; su densidad es asintóticamente proporcional a . En los mismos términos, demuestra "aleatoriedad moderada marginal". Por ello, la distribución normal sesgada es útil para modelar distribuciones sesgadas que no tienen más valores atípicos que la normal, mientras que la distribución normal modificada exponencialmente es útil para casos con un mayor número de casos atípicos en una sola dirección.
Implementaciones[editar]
Existe una implementación en R para la función de densidad, de distribución, de cuantiles y para generar desviaciones aleatorias en https://cran.r-project.org/web/packages/sn/index.html.
Véase también[editar]
Referencias[editar]
- ↑ O'HAGAN, A.; LEONARD, TOM (1976). «Bayes estimation subject to uncertainty about parameter constraints». Biometrika 63 (1): 201-203. ISSN 0006-3444. doi:10.1093/biomet/63.1.201.
- ↑ Ashour, Samir K.; Abdel-hameed, Mahmood A. (October 2010). «Approximate skew normal distribution». Journal of Advanced Research 1 (4): 341-350. ISSN 2090-1232. doi:10.1016/j.jare.2010.06.004.
- ↑ Mudholkar, Govind S.; Hutson, Alan D. (February 2000). «The epsilon–skew–normal distribution for analyzing near-normal data». Journal of Statistical Planning and Inference 83 (2): 291-309. ISSN 0378-3758. doi:10.1016/s0378-3758(99)00096-8.
- ↑ Andel, J., Netuka, I. and Zvara, K. (1984) On threshold autoregressive processes. Kybernetika, 20, 89-106
- ↑ Chan, K. S.; Tong, H. (March 1986). «A note on certain integral equations associated with non-linear time series analysis». Probability Theory and Related Fields 73 (1): 153-158. ISSN 0178-8051. S2CID 121106515. doi:10.1007/bf01845999.
- ↑ Azzalini, A. (1985). «A class of distributions which includes the normal ones». Scandinavian Journal of Statistics 12: 171-178.
- ↑ Azzalini, Adelchi; Capitanio, Antonella (2014). The skew-normal and related families. pp. 32-33. ISBN 978-1-107-02927-9.
- ↑ Pewsey, Arthur (1 de septiembre de 2000). «Problems of inference for Azzalini's skewnormal distribution». Journal of Applied Statistics 27 (7): 859-870. ISSN 0266-4763. doi:10.1080/02664760050120542.
Enlaces externos[editar]
- Azzalini, A (1 de diciembre de 1996). «The multivariate skew-normal distribution». Biometrika 83 (4): 715-726. ISSN 0006-3444,1464-3510
|issn=incorrecto (ayuda). doi:10.1093/biomet/83.4.715. - Una muy breve introducción a la distribución normal sesgada (en inglés)
- La distribución normal sesgada (y distribuciones relacionadas, como la t sesgada) (en inglés)
- Función T de Owens (en inglés)
- Distribuciones cerradas sesgadas - Simulación, inversión y estimación de parámetros Archivado el 14 de agosto de 2011 en Wayback Machine. (en inglés)
- Esta obra contiene una traducción derivada de «Skew normal distribution» de Wikipedia en inglés, concretamente de esta versión del 7 de mayo de 2021, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.






![{\displaystyle \Phi (x)=\int _{-\infty }^{x}\phi (t)\ dt={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b64168aa76f440a9ab0071082ed917dee8b8a4b6)
































