Diferencia entre revisiones de «Teorema de Tales»
'''Texto en negrita''' |
m Revertidos los cambios de 201.252.35.253 a la última edición de Diegusjaimes |
||
| Línea 1: | Línea 1: | ||
Existen dos teoremas que reciben el nombre de '''Teorema de Tales'''. |
|||
=== Primer teorema === |
|||
[[Imagen:Thales theorem 7.png|thumb|Una aplicación del Teorema de Tales]] |
|||
Si a un triángulo cualquiera le trazamos una paralela a cualquiera de sus lados, obtenemos 2 triángulos semejantes. Dos triángulos son semejantes si tienen los ángulos iguales y sus lados son proporcionales, es decir, que la igualdad de los cocientes equivale al paralelismo. Este teorema establece así una relación entre el álgebra y la geometría. |
|||
La primera figura corresponde a medidas algebraicas positivas - los vectores ''OA'', ''OA<nowiki>'</nowiki>'', ''OB'' y ''OB<nowiki>'</nowiki>'' tienen la misma orientación que la rectas ''(d)'' y ''(d')'', y la segunda a cocientes negativos. |
|||
Si se aplica el teorema, tenemos además otra consecuencia: si se orienta de la misma manera las dos rectas paralelas ''(AB)'' y ''(A'B')'', es decir con el mismo vector, entonces el tercer cociente (de medidas algebraicas): ''A'B<nowiki>'</nowiki>'' / ''AB'' es igual a los dos anteriores. |
|||
A veces se reserva el nombre de ''teorema de Tales'' al sentido directo de la equivalencia, y el otro sentido recibe el nombre de ''recíproca del teorema de Tales''. |
|||
Este teorema es un caso particular de los [[Triángulos semejantes|triángulos similares o semejantes]]. |
|||
Una aplicación interesante es para medir la altura de un árbol. |
|||
# Medimos la longitud de su sombra a una hora determinada. = C |
|||
# Medimos la longitud de la sombra de un objeto pequeño (por ejemplo un lápiz) en el mismo instante. = B |
|||
# Medimos la longitud real del mismo cuerpo. = A |
|||
Y obtenemos <math>D = C \left(\frac{A}{B}\right)</math> donde D es la altura real del árbol. |
|||
También se puede relacionar para medir una distancia, cuya finidad no pueda ser medida, y apoyándose en un punto. |
|||
== Segundo teorema == |
|||
[[imagen:ES-Teorema de Tales de Mileto.svg|thumb|Ilustración del enunciado del segundo teorema de Tales de Mileto]] |
|||
El segundo teorema de Tales de Mileto es un teorema de [[geometría]] particularmente enfocado a los [[triángulos rectángulos]], las [[circunferencia|circunferencias]] y los [[Angulo#.C3.81ngulos_respecto_de_una_circunferencia|ángulos inscritos]], consiste en el siguiente enunciado: |
|||
{{teorema |
|||
|1= Sea C un punto de la circunferencia de diámetro [AB], distinto de A y de B. Entonces el ángulo ACB, es [[ángulo recto|recto]]. |
|||
|2=[[Tales de Mileto]] |
|||
}} |
|||
Este teorema es un caso particular de una propiedad de los [[puntos cocíclicos]] y de la aplicación de los [[Angulo#.C3.81ngulos_respecto_de_una_circunferencia|ángulos inscritos]] dentro de una circunferencia. |
|||
'''Comprobación''': OA = OB = OC = r, siendo O el punto central del círculo y r el [[radio (geometría)|radio]] de la circunferencia. Por lo tanto OAC y OBC son isósceles. La suma de los ángulos del triángulo ABC es equivalente a <math>2 \alpha + 2 \beta = \pi</math> (radianes). Dividiendo por dos, se obtiene:</br> |
|||
<math><\!BCA\!> \ = \alpha + \beta = \frac {\pi} 2 </math> (o 90º). |
|||
Además, la [[bisectriz]] de un [[triángulo]] corta al lado opuesto del [[ángulo]] con la bisectriz en dos segmentos iguales. Hipotenusa² = C² + C², es decir AB²=CA²+CB². |
|||
En conclusión se forma un triángulo rectángulo. |
|||
== El Primer Teorema de Tales en la cultura popular == |
|||
El grupo musical argentino [[Les Luthiers]] compuso e interpretó una canción dedicada al Primer Teorema de Tales.<ref>[http://www.youtube.com/watch?v=czzj2C4wdxY El Teorema de Thales por Les Luthiers en You Tube]</ref> |
|||
Franco nocete |
|||
cuando dos rectas están cortadas por varias paralelas, se determinan segmentos propocionales y las figuras que se forman se dice que están en proporción de thales. |
|||
== Véase también == |
|||
* [[Tales de Mileto]] |
|||
El teorema de Tales es una fórmula que se utiliza en geometría proporcional y raccional. |
|||
== Referencias == |
|||
{{listaref|1}} |
|||
{{bueno|fr}} |
|||
[[Categoría:Teoremas de geometría]] |
|||
[[Categoría:Triángulos]] |
|||
[[ar:نظرية طالس]] |
|||
[[bg:Теорема на Талес]] |
|||
[[ca:Teorema de Tales]] |
|||
[[cs:Thaletova věta]] |
|||
[[de:Satz des Thales]] |
|||
[[en:Thales' theorem]] |
|||
[[fi:Thaleen lause]] |
|||
[[fr:Théorème de Thalès (cercle)]] |
|||
[[he:משפט תאלס]] |
|||
[[hu:Thalész-tétel]] |
|||
[[it:Teorema di Talete]] |
|||
[[nds:Satz vun Thales]] |
|||
[[nl:Stelling van Thales]] |
|||
[[pl:Twierdzenie Talesa]] |
|||
[[pt:Teorema de Tales]] |
|||
[[ro:Teorema lui Thales]] |
|||
[[ru:Теорема Фалеса]] |
|||
[[sl:Talesov izrek]] |
|||
[[sr:Талесова теорема]] |
|||
[[uk:Теорема Фалеса]] |
|||
[[zh:泰勒斯定理]] |
|||
Revisión del 22:09 26 ago 2009
Existen dos teoremas que reciben el nombre de Teorema de Tales.
Primer teorema
Si a un triángulo cualquiera le trazamos una paralela a cualquiera de sus lados, obtenemos 2 triángulos semejantes. Dos triángulos son semejantes si tienen los ángulos iguales y sus lados son proporcionales, es decir, que la igualdad de los cocientes equivale al paralelismo. Este teorema establece así una relación entre el álgebra y la geometría.
La primera figura corresponde a medidas algebraicas positivas - los vectores OA, OA', OB y OB' tienen la misma orientación que la rectas (d) y (d'), y la segunda a cocientes negativos.
Si se aplica el teorema, tenemos además otra consecuencia: si se orienta de la misma manera las dos rectas paralelas (AB) y (A'B'), es decir con el mismo vector, entonces el tercer cociente (de medidas algebraicas): A'B' / AB es igual a los dos anteriores.
A veces se reserva el nombre de teorema de Tales al sentido directo de la equivalencia, y el otro sentido recibe el nombre de recíproca del teorema de Tales.
Este teorema es un caso particular de los triángulos similares o semejantes.
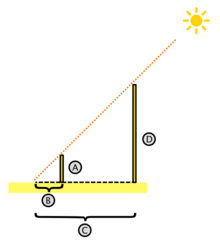
Una aplicación interesante es para medir la altura de un árbol.
- Medimos la longitud de su sombra a una hora determinada. = C
- Medimos la longitud de la sombra de un objeto pequeño (por ejemplo un lápiz) en el mismo instante. = B
- Medimos la longitud real del mismo cuerpo. = A
Y obtenemos donde D es la altura real del árbol.
También se puede relacionar para medir una distancia, cuya finidad no pueda ser medida, y apoyándose en un punto.
Segundo teorema

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:
|
Este teorema es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.
Comprobación: OA = OB = OC = r, siendo O el punto central del círculo y r el radio de la circunferencia. Por lo tanto OAC y OBC son isósceles. La suma de los ángulos del triángulo ABC es equivalente a (radianes). Dividiendo por dos, se obtiene:
(o 90º).
Además, la bisectriz de un triángulo corta al lado opuesto del ángulo con la bisectriz en dos segmentos iguales. Hipotenusa² = C² + C², es decir AB²=CA²+CB².
En conclusión se forma un triángulo rectángulo.
El Primer Teorema de Tales en la cultura popular
El grupo musical argentino Les Luthiers compuso e interpretó una canción dedicada al Primer Teorema de Tales.[1] Franco nocete
cuando dos rectas están cortadas por varias paralelas, se determinan segmentos propocionales y las figuras que se forman se dice que están en proporción de thales.
Véase también
El teorema de Tales es una fórmula que se utiliza en geometría proporcional y raccional.



