Diferencia entre revisiones de «Altura (geometría)»
Sin resumen de edición |
m Revertidos los cambios de 189.243.23.32 a la última edición de Africanus |
||
| Línea 7: | Línea 7: | ||
La magnitud de la [[altura]] sirve para calcular el [[área]] de un [[triángulo]], siendo su valor: '''a = b·h/2''', donde '''a''' es el área, '''b''' la base –la [[longitud]] del lado "inferior"–, y '''h''' su altura correspondiente. |
La magnitud de la [[altura]] sirve para calcular el [[área]] de un [[triángulo]], siendo su valor: '''a = b·h/2''', donde '''a''' es el área, '''b''' la base –la [[longitud]] del lado "inferior"–, y '''h''' su altura correspondiente. |
||
(Esto |
|||
En la figura, pueden ser BC·AA"/2, AB·CC"/2 o AC·BB"/2. |
En la figura, pueden ser BC·AA"/2, AB·CC"/2 o AC·BB"/2. |
||
| Línea 21: | Línea 20: | ||
* las alturas contienen a las [[mediatrices]] del triángulo A'B'C' (que se construye trazando paralelas a los lados por los vértices opuestos); |
* las alturas contienen a las [[mediatrices]] del triángulo A'B'C' (que se construye trazando paralelas a los lados por los vértices opuestos); |
||
* el ortocentro del triángulo ACB es el [[circuncentro]] del triángulo A'B'C'. |
* el ortocentro del triángulo ACB es el [[circuncentro]] del triángulo A'B'C'. |
||
Por esto empezo la rebelion de manuel roberto ordoñez. |
|||
[[Categoría:Triángulos]] |
[[Categoría:Triángulos]] |
||
Revisión del 23:13 26 abr 2010
Altura de un triángulo, respecto de un lado, es la distancia más corta entre la recta que contiene al lado y el vértice opuesto. Equivale a un segmento perpendicular a dicho lado con un extremo en el vértice opuesto y el otro en dicho lado, o en su prolongación.

En la figura, las alturas respecto de sus tres lados BC, CA y AB" son AA", BB" y CC".
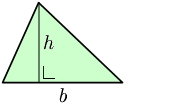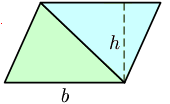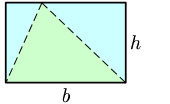
La magnitud de la altura sirve para calcular el área de un triángulo, siendo su valor: a = b·h/2, donde a es el área, b la base –la longitud del lado "inferior"–, y h su altura correspondiente.
En la figura, pueden ser BC·AA"/2, AB·CC"/2 o AC·BB"/2.
Ésta fórmula se puede demostrar, geométricamente, trazando un rectángulo cuya área es el doble del área del triángulo, con la misma base y la misma altura.
Características y propiedades de las alturas del triángulo
En todo triángulo:
- al menos una de las alturas se encuentra dentro del triángulo;
- la altura de mayor longitud es la correspondiente a la del lado menor del triángulo;
- las tres alturas se cortan en un punto, llamado ortocentro del triángulo (H en el gráfico);
- las alturas contienen a las mediatrices del triángulo A'B'C' (que se construye trazando paralelas a los lados por los vértices opuestos);
- el ortocentro del triángulo ACB es el circuncentro del triángulo A'B'C'.
