Polinomio de Wilkinson
En análisis numérico, un polinomio de Wilkinson es un tipo de polinomio específico utilizado por James H. Wilkinson en 1963 para ilustrar la dificultad de encontrar las raíces de un polinomio, dado que su ubicación puede ser muy sensible a pequeñas variaciones en los coeficientes del propio polinomio.
La expresión del polinomio es:
A veces, el término polinomio de Wilkinson también se usa para referirse a otros polinomios que aparecen en los análisis realizados por Wilkinson.
Antecedentes[editar]
El polinomio de Wilkinson surgió en el estudio de algoritmos para encontrar las raíces de un polinomio
Es una cuestión natural en el análisis numérico preguntar si el problema de encontrar las raíces de un polinomio p a partir de sus coeficientes ci es una tarea bien condicionada. Es decir, que un pequeño cambio en los coeficientes implique un pequeño cambio en las raíces. Desafortunadamente, este no es el caso analizado por Wilkinson.
El problema está mal condicionado cuando el polinomio tiene una raíz múltiple. Por ejemplo, el polinomio x2 tiene una raíz doble en x = 0. Sin embargo, el polinomio x2 − ε (una perturbación de tamaño ε) tiene raíces en ±√ε, que es mucho más grande que ε cuando ε es pequeño.
Por lo tanto, es natural esperar que también ocurra un mal condicionamiento cuando el polinomio tiene ceros que están muy cerca. Sin embargo, el problema también puede estar extremadamente mal condicionado para polinomios con ceros bien separados. Wilkinson usó el polinomio w(x) para ilustrar este punto (Wilkinson 1963).
En 1984, describió el impacto que le causó este descubrimiento:
- "Personalmente, la considero la experiencia más traumática de mi carrera como analista numérico".[1]
El polinomio de Wilkinson se usa a menudo para ilustrar lo indeseable de calcular ingenuamente los autovalores de una matriz calculando primero los coeficientes del polinomio característico de la matriz y luego encontrando sus raíces, ya que usar los coeficientes como un paso intermedio puede introducir un mal condicionamiento extremo incluso si el problema original estaba bien condicionado.[2]
Condicionado del polinomio de Wilkinson[editar]
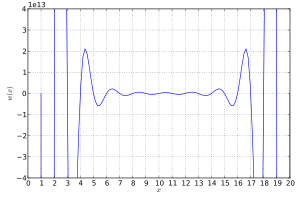
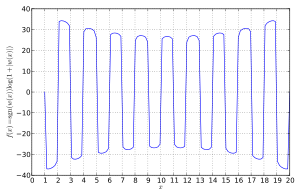
El polinomio de Wilkinson
claramente tiene 20 raíces, ubicadas en x = 1, 2, ..., 20. Estas raíces están muy separadas. Sin embargo, el polinomio todavía está muy mal condicionado.
Ampliando el polinomio, se encuentra que
Si se modifica en una pequeña cantidad el coeficiente de x19, cambiándolo de −210 a −210.0000001192 (=-210-2−23), entonces el valor polinomial w(20) disminuye de 0 a −2−232019 =−6.25×1017, y la raíz en x =20 crece hasta x ≈20.8. Las raíces en x =18 y x =19 se encuentran con una raíz doble en x≈18.62, que se convierte en un par de raíces conjugadas complejas en x≈19.5 ± 1.9i a medida que la perturbación aumenta aún más. Las 20 raíces se convierten (con 5 decimales) en:
Algunas de las raíces están muy desplazadas, aunque el cambio en el coeficiente es pequeño y las raíces originales parecen estar muy espaciadas. Wilkinson demostró mediante el análisis de estabilidad discutido en la siguiente sección que este comportamiento está relacionado con el hecho de que algunas raíces α (como α =15) tienen muchas raíces β que son "cerradas" en el sentido de que |α - β| es más pequeño que |α|.
Wilkinson eligió la perturbación de 2−23 porque su computadora Pilot ACE usaba números de coma flotante con una mantisa de 30 bits, por lo que para números de alrededor de 210, al añadir 2−23 se alcanzaba la primera posición de bit no representable por la computadora. Los dos números reales, −210 y −210−2−23, están representados por el mismo número de coma flotante, lo que significa que 2−23 era el error "inevitable" al representar un coeficiente real cercano a −210 mediante un número de coma flotante en su computadora. El análisis de perturbación demuestra que manejar los coeficientes con precisión de 30 bits es insuficiente para separar las raíces del polinomio de Wilkinson.
Análisis de estabilidad[editar]
Supóngase que se perturba un polinomio p(x) = Π(x − αj) con raíces αj agregando un pequeño múltiplo t·c(x) de un polinomio c(x), y véase cómo afecta esto a las raíces αj. En una primera aproximación, el cambio en las raíces será controlado por la derivada
Cuando la derivada es grande, las raíces serán menos estables bajo variaciones de t y, a la inversa, si esta derivada es pequeña, las raíces serán estables. En particular, si αj es una raíz múltiple, el denominador desaparece. En este caso, αj generalmente no es diferenciable con respecto a t (a menos que c desaparezca aquí), y las raíces serán extremadamente inestables.
Para valores pequeños de t, la raíz perturbada está dada por la expansión de la serie de potencias en t
y son de esperar problemas cuando |t| es mayor que el radio de convergencia de esta serie de potencias, que viene dado por el valor más pequeño de |t| de modo que la raíz αj se vuelva múltiple. Una estimación muy burda de este radio toma la mitad de la distancia desde αj a la raíz más cercana y dividido por la derivada anterior.
En el ejemplo del polinomio de Wilkinson de grado 20, las raíces están dadas por αj =j para j = 1, ..., 20 y c(x) es igual a x19. Entonces, la derivada viene dada por
Esto demuestra que la raíz αj será menos estable si hay muchas raíces αk cerca de αj, en el sentido de que la distancia |αj − αk| entre ellos es menor que |αj|.
Ejemplo. Para la raíz α1 = 1, la derivada es igual a 1/19!, que es un número muy pequeño; esta raíz es estable incluso para grandes cambios en t. Esto se debe a que todas las demás raíces β están muy lejos de ella, en el sentido de que |α1 − β| = 1, 2, 3, ..., 19 es mayor que |α1| = 1. Por ejemplo, incluso si t es tan grande como –10000000000, la raíz α1 solo cambia de 1 a aproximadamente 0,99999991779380 (que está muy cerca de la aproximación de primer orden 1 + t/19! ≈ 0.99999991779365). Del mismo modo, las otras raíces pequeñas del polinomio de Wilkinson son insensibles a los cambios en t.
Ejemplo. Por otro lado, para la raíz α20 = 20, la derivada es igual a −2019/19! que es enorme (alrededor de 43000000), por lo que esta raíz es muy sensible a pequeños cambios en t. Las otras raíces β están cercanas a α20, en el sentido de que |β − α20| = 1, 2, 3, ..., 19 es menor que |α20| = 20. Para t = −2 − 23 la aproximación de primer orden 20 − t·2019/19! = 25.137 ... a la raíz perturbada 20.84 ... es muy deficiente; esto es aún más obvio para la raíz α19, donde la raíz perturbada tiene una gran parte imaginaria pero la aproximación de primer orden (y para el caso todas las aproximaciones de orden superior) son reales. La razón de esta discrepancia es que |t| ≈ 0.000000119 es mayor que el radio de convergencia de la serie de potencias mencionada anteriormente (que es aproximadamente 0.0000000029, algo menor que el valor 0.00000001 dado por la estimación bruta) por lo que la teoría linealizada no se aplica. Para un valor como t = 0.000000001 que es significativamente más pequeño que este radio de convergencia, la aproximación de primer orden 19.9569 ... está razonablemente cerca de la raíz 19.9509 ...
A primera vista, las raíces α1 = 1 y α20 = 20 del polinomio de Wilkinson parecen ser similares, ya que están en extremos opuestos de una línea simétrica de raíces y tienen el mismo conjunto de distancias. 1, 2, 3, ..., 19 de otras raíces. Sin embargo, el análisis anterior demuestra que esto es extremadamente engañoso: la raíz α20 = 20 es menos estable que α1 = 1 (a pequeñas perturbaciones en el coeficiente de x19) por un factor de 2019 = 5242880000000000000000000.
Segundo ejemplo de Wilkinson[editar]
El segundo ejemplo considerado por Wilkinson es
Los veinte ceros de este polinomio están en una progresión geométrica con razón común 2, y por lo tanto el cociente
no puede ser grande. De hecho, los ceros de w2 son bastante estables a grandes cambios relativos en los coeficientes.
Efecto de la base[editar]
La expansión
expresa el polinomio en una base particular, a saber, la de los monomios. Si el polinomio se expresa en otra base, entonces el problema de encontrar sus raíces puede dejar de estar mal condicionado. Por ejemplo, en una forma de Lagrange, un pequeño cambio en uno (o varios) coeficientes no implica modificaciones demasiado grandes en las raíces. De hecho, los polinomios base para la interpolación en los puntos 0, 1, 2, ..., 20 son
Cada polinomio (de grado 20 o menos) se puede expresar en esta base:
Para el polinomio de Wilkinson, se tiene que
Dada la definición del polinomio de base de Lagrange ℓ0 (x), un cambio en el coeficiente d0 no producirá ningún cambio en las raíces de w. Sin embargo, una perturbación en los otros coeficientes (todos iguales a cero) cambiará ligeramente las raíces. Por lo tanto, el polinomio de Wilkinson está bien condicionado en esta base.
Publicaciones[editar]
Wilkinson discutió "su" polinomio en
- J. H. Wilkinson (1959). "The evaluation of the zeros of ill-conditioned polynomials. Part I." (La evaluación de los ceros de polinomios mal condicionados. Parte I.)Numerische Mathematik 1:150-166.
- J. H. Wilkinson (1963). "Rounding Errors in Algebraic Processes" (Errores de redondeo en procesos algebraicos). Englewood Cliffs, Nueva Jersey: Prentice Hall.
Referencias[editar]
- ↑ Wilkinson, James H. (1984). «The perfidious polynomial». En Gene H. Golub, ed. Studies in Numerical Analysis. Mathematical Association of America. pp. 3. ISBN 978-0-88385-126-5.
- ↑ Trefethen, Lloyd N.; Bau, David (1997), Numerical Linear Algebra, SIAM.
Bibliografía[editar]
El trabajo de Wilkinson se menciona en libros de texto estándar de análisis numérico, como:
- F. S. Acton, "Numerical methods that work" (Métodos numéricos que funcionan), ISBN 978-0-88385-450-1, p. 201.
Otras referencias:
- Ronald G. Mosier (julio de 1986). "Root neighborhoods of a polynomial" (Raíces vecinas de un polinomio). Mathematics of Computation (Matemáticas de la Computación) 47 (175): 265-273.
- J. H. Wilkinson (1984). El polinomio pérfido. "Estudios en análisis numérico", ed. por G. H. Golub, págs. 1–28. (Estudios de Matemáticas, vol. 24). Washington, D.C.: Asociación Matemática de América.
Se presenta un cálculo numérico de alta precisión en:
- Ray Buvel, Polinomios y funciones racionales, parte del RPN Calculator User Manual (para Python), consultado el 29 de julio de 2006.





![{\displaystyle {\begin{array}{rrrrr}1.00000&2.00000&3.00000&4.00000&5.00000\\[8pt]6.00001&6.99970&8.00727&8.91725&20.84691\\[8pt]10.09527\pm {}&11.79363\pm {}&13.99236\pm {}&16.73074\pm {}&19.50244\pm {}\\[-3pt]0.64350i&1.65233i&2.51883i&2.81262i&1.94033i\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9ef3ed5ccf6888e074b040621f05213aa519e04)








