Problema del círculo mínimo

Algunas ejemplos del círculos de recubrimiento mínimo.

El problema del círculo mínimo (también conocido como el problema del círculo de recubrimiento mínimo) es una cuestión matemática, consistente en calcular la circunferencia más pequeña que contiene todo un conjunto de puntos dado en el plano. El problema correspondiente en el espacio n-dimensional, implica determinar la n-esfera más pequeña que contiene todos los puntos de un conjunto dado.​ El problema del círculo mínimo fue propuesto inicialmente por el matemático inglés James Joseph Sylvester en 1857.​

En el plano es un ejemplo de un problema de localización de servicios (el problema del 1-centro) en el que se debe elegir la ubicación de una nueva instalación para proporcionar servicio a un determinado número de clientes, minimizando la distancia más larga que cualquier cliente debe recorrer para alcanzar el nueva instalación.​ Tanto el problema de círculo mínimo en el plano como el problema de la esfera mínima en cualquier espacio de dimensión superior finita se pueden resolver con rutinas en tiempo lineal.

Caracterización

La mayoría de los enfoques geométricos para el problema buscan puntos que se encuentran en el límite del círculo mínimo y se basan en los siguientes hechos simples:

• El círculo de cobertura mínimo es único.
• El círculo de cobertura mínimo de un conjunto S puede determinarse por un máximo de tres puntos en S, que se encuentran en el límite del círculo. Si solo está determinado por dos puntos, entonces el segmento de línea que une esos dos puntos debe ser un diámetro del círculo mínimo. Si está determinado por tres puntos, entonces el triángulo formado por esos tres puntos no es obtuso.

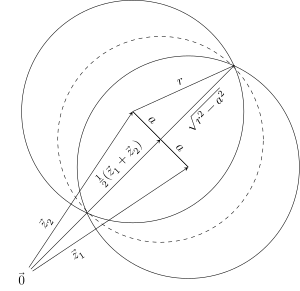
Demostración de que el disco de cobertura mínimo es único

Sea P un conjunto cualquiera de puntos en el plano, y supóngase que hay dos discos más pequeños que recubren P, con centros en ${\vec {z}}_{1}$ y ${\vec {z}}_{2}$. Sea r su radio compartido y sea $2a$ la distancia entre sus centros. Entonces, dado que P es un subconjunto de ambos discos, es un subconjunto de su intersección. Sin embargo, su intersección está contenida dentro del disco con el centro ${\frac {1}{2}}({\vec {z}}_{1}+{\vec {z}}_{2})$ y el radio ${\sqrt {r^{2}-a^{2}}}$, como se muestra en la siguiente imagen: Como r es mínimo, entonces ${\sqrt {r^{2}-a^{2}}}=r$, lo que significa que $a=0$, por lo que los discos son idénticos.​

Soluciones en tiempo lineal

Como Nimrod Megiddo demostró,​ el círculo delimitador mínimo se puede encontrar en tiempo lineal, y el mismo límite de tiempo lineal también se aplica a la esfera mínima envolvente en espacios euclidianos de cualquier dimensión finita.

Emo Welzl​ propuso un algoritmo aleatorio simple para el problema del círculo mínimo de cobertura, que se ejecuta en el tiempo esperado $O(N)$, basado en un algoritmo de programación lineal de Raimund Seidel. Este algoritmo se presenta a continuación.

Posteriormente, el problema del círculo mínimo se incluyó en una clase general de problemas tipo LP, que se puede resolver con algoritmos como el basado en la programación lineal de Welzl. Como consecuencia de pertenecer a esta clase, se demostró que la dependencia de la dimensión del factor constante en el límite de tiempo de $O(N)$, que era factorial para el método de Seidel, podría reducirse a subexponencial, mientras que todavía se mantiene solo la dependencia lineal de N.​

El algoritmo de Welzl

El algoritmo es recursivo y toma como argumentos dos conjuntos (finitos) de puntos P y R; calcula el círculo delimitador más pequeño de la unión de P y de R, siempre que cada punto de R sea uno de los puntos límite del eventual círculo delimitador más pequeño. Por lo tanto, el problema del círculo circundante más pequeño original puede resolverse llamando al algoritmo con P igual al conjunto de puntos que se van a encerrar y R igual al conjunto vacío; como el algoritmo se llama recursivamente, ampliará el conjunto R mediante sucesivas llamadas recursivas hasta que incluya todos los puntos límite del círculo.

El algoritmo procesa los puntos de P en un orden aleatorio, manteniendo como lo hace el conjunto S de puntos procesados y el círculo más pequeño D que encierra la unión S ∪ R. En cada paso, prueba si el siguiente punto p para ser procesado está en D; si no, el algoritmo reemplaza el D por el resultado de una llamada recursiva del algoritmo en los conjuntos S y R ∪ p. En función de si el círculo fue reemplazado o no, p se incluye en el conjunto S. El procesamiento de cada punto, por lo tanto, consiste en probar en tiempo constante si el punto pertenece a un solo círculo y posiblemente realizar una llamada recursiva al algoritmo. Se puede demostrar que el tiempo total es lineal.

algorithm welzl:​
    input: Finite sets P and R of points in the plane
    output: Minimal disk enclosing P with R on the boundary, or undefined if no such disk exists
    if P is empty or |R| ≥ 3:
        if |R| = 1:
            (we do this to support multisets with duplicate points)
            (we assume that a circle with a radius of zero can exist)
            p := R[0]
            return circle(p, 0)
        else if |R| = 2:
            (we do this to support multisets with duplicate points)
            (we use that the smallest circle between two points has a center at their midpoint)
            (and the segment that passes through them is a diameter of the circle)
            p0 := R[0]
            p1 := R[1]
            center := midpoint(p0, p1)
            diameter := distance(p0, p1)
            return circle(center, diameter / 2)
        else if the points of R are cocircular:
            return the ball they determine
        else:
            return undefined

    choose p in P (randomly and uniformly)
    D := welzl(P - { p }, R)
    if p is in D:
        return D
    return welzl(P - { p }, R ∪ { p })

Otros algoritmos

Antes del resultado de Megiddo que muestra que el problema del círculo mímo se puede resolver en tiempo lineal, se idearon varios algoritmos de mayor complejidad. Un algoritmo ingenuo resuelve el problema en el tiempo O (n⁴) probando los círculos determinados por todos los pares y triples de puntos.

• Un algoritmo de Chrystal y Peirce aplica una estrategia optimización local que mantiene dos puntos en el límite de un círculo circundante y reduce repetidamente el círculo, reemplazando el par de puntos límite, hasta que se encuentra un círculo óptimo. Chakraborty y Chaudhuri​ proponen un método de tiempo lineal para seleccionar un círculo inicial adecuado y un par de puntos límite en ese círculo. Cada paso del algoritmo incluye como uno de los dos puntos límite un nuevo vértice de la envolvente convexa, por lo que si el contorno tiene h vértices, este método puede implementarse para ejecutarse en el tiempo O (nh).

• Elzinga y Hearn​ describieron un algoritmo que mantiene un círculo de cobertura para un subconjunto de los puntos. En cada paso, un punto no cubierto por la esfera actual se utiliza para encontrar una esfera más grande que cubra un nuevo subconjunto de puntos, incluido el punto encontrado. Aunque su peor tiempo de ejecución es O (h³n), los autores informan que se ejecutó en tiempo lineal en sus experimentos. La complejidad del método ha sido analizada por Drezner y Shelah.​ Ambos códigos Fortran y C están disponibles en Hearn, Vijay y Nickel (1995).​

• El problema de la esfera mínima se puede formular como un programa cuadrático​ definido por un sistema de restricciones lineales con una función objetivo cuadrática convexa. Por lo tanto, cualquier algoritmo de dirección factible puede dar la solución al problema.​ Hearn y Vijay​ demostraron que el enfoque de dirección factible elegido por Jacobsen es equivalente al algoritmo de Chrystal-Peirce.

• El dual a este programa cuadrático también se puede formular explícitamente:​ un algoritmo de Lawson​ se puede describir de esta manera como un algoritmo dual primario.​

• Shamos y Hoey​ propusieron un algoritmo de tiempo O (n log n) para el problema basado en la observación de que el centro del círculo delimitador más pequeño debe ser un vértice del punto más alejado de los polígonos de Thiessen del conjunto de puntos de entrada.

Variaciones ponderadas del problema

La versión ponderada del problema del círculo de cobertura mínimo toma como entrada un conjunto de puntos en un espacio euclidiano, cada uno con pesos; el objetivo es encontrar un único punto que minimice la distancia máxima ponderada a cualquier punto. El problema original mínimo del círculo de cobertura puede recuperarse estableciendo todos los pesos en el mismo número. Al igual que con el problema no ponderado, el problema ponderado puede resolverse en tiempo lineal en cualquier espacio de dimensión limitada, utilizando enfoques estrechamente relacionados con los algoritmos de programación lineal de acotación limitada, aunque los algoritmos más lentos vuelven a ser frecuentes en la literatura.​​​

Véase también

• Esfera envolvente
• Circunferencia circunscrita
• Cadena más próxima

Enlaces externos

• El código de bola más pequeño de Bernd Gärtner
• CGAL el paquete Min_sphere_of_spheres de la Biblioteca de Algoritmos de Geometría Computacional (CGAL)
• Miniball una implementación de fuente abierta de un algoritmo para el problema de bola envolvente mínima para dimensiones bajas y moderadamente altas

• Datos: Q2591189
• Multimedia: Smallest circle problem / Q2591189